Теоретические основы

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЗАКОН СОХРАНЕНИЯ ЗАРЯДА. ЗАКОН КУЛОНА. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Теоретические основы

В электростатике рассматриваются свойства и взаимодействия неподвижных в инерциальной системе отсчёта электрически заряженных тел или частиц, обладающих электрическим зарядом.

Электрический заряд это физическая величина, характеризующая свойство заряженных частиц или тел вступать в электромагнитные взаимодействия и определяющая величину сил и энергий при таких взаимодействиях.

Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. В природе существуют два вида электрических зарядов. Условно их называют положительными и отрицательными. Заряды одного знака отталкиваются, разных знаков – притягиваются друг к другу. Самым маленьким является заряд элементарных частиц. Этот заряд называется элементарным. Абсолютное значение элементарного заряда 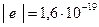Кл. Устойчивыми частицами, которые входят в состав любого вещества, являются электрон (элементарный заряд отрицательный) и протон (элементарный заряд положительный).

Если каким либо образом создать в теле избыток частиц одного знака, то тело окажется заряженным. Электрический заряд квантуется. Заряженное тело имеет заряд q, который равен целому числу элементарных зарядов, т.е. 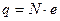, где N – число элементарных зарядов. [N]=безразмерная величина, [q]= Кл, [e]= Кл.

Заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других тел, с которыми он взаимодействует, называется точечным зарядом.

Величина заряда, измеряемая в различных инерциальных системах отсчёта, оказывается одинаковой.

Система называется электрически изолированной, если через ограничивающую её поверхность не могут проникать заряженные частицы.

Закон сохранения электрического заряда.

В электрически изолированной системе взаимодействующих заряженных тел, алгебраическая сумма электрических зарядов остаётся постоянной.

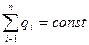, (1.1)

где: q_i – i-ый заряд системы, 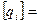Кл; п - число зарядов.

Закон сохранения электрического заряда является фундаментальным и тесно связан с релятивистской инвариантностью заряда.

Закон Кулона

Закон Кулонасправедлив для взаимодействия неподвижных точечных зарядов, а также заряженных тел шарообразной формы, если их заряды равномерно распределены по всему объёму или по всей поверхности этих тел.

Формулировка закона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния между ними

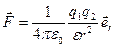, (1.2)

где 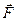– сила взаимодействия зарядов q₁ и q₂; r расстояние между зарядами; ε_о – электрическая постоянная, ε – диэлектрическая проницаемость среды; 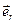– орт-вектор направления действия силы.

Линейная плотность заряда

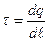, (1.3)

Поверхностная плотность заряда

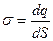, (1.4)

Объёмная плотность заряда

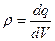, (1.5)

где dq – элементарный заряд; dl, dS, dV – элементы длины, площади и объема.

Электрическое поле.

Всякий электрический заряд или заряженное тело изменяет свойства окружающего его пространства, создавая в нём электрическое поле. Электрическое поле проявляет себя в действии силы на электрический заряд, помещённый в какую-либо точку этого поля.

Векторной силовой характеристикой электрического поля является напряжённость поля.

Напряженность электрического поля

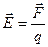, (1.6)

здесь q - заряд, помещенный в электрическом поле (пробный заряд).

Пробный заряд должен быть настолько мал, чтобы он не мог исказить исследуемое с его помощью поле.

Если q > 0, вектор 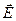направлен по 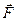; если q < 0, векторы 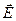и и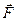меют противоположные направления.

Напряженность поля точечного заряда в вакууме

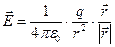, (1.7)

где 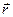– радиус-вектор, соединяющий заряд q с точкой, в которой вычисляется напряженность поля; q – точечный заряд, создающий поле; 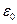– электрическая постоянная.

Если q > 0, вектор 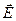направлен по радиус-вектору от заряда; если q < 0 – к заряду (см. рис.1).

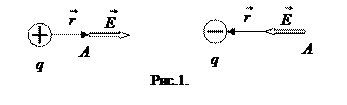
Однородное электрическое поле – поле, в каждой точке которого напряженность 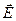одинакова по величине и направлению.

Если 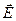не зависит от времени – однородное поле является стационарным (или постоянным).

Поле точечного заряда – неоднородное.

Принцип суперпозиции электрических полей: Напряженность электрического поля системы точечных зарядов в любой точке пространства равна геометрической сумме напряженностей полей каждого из этих зарядов в отдельности.

Заряды в пространстве распределяются либо дискретно, либо непрерывно.

· В случае дискретного распределения электрических зарядов:

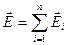, (1.8)

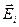где – напряженность, создаваемая i-м зарядом в рассматриваемой точке поля, n – число дискретных зарядов, входящих в состав системы.

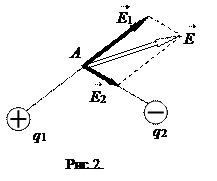
· Напряженность поля в точке А, создаваемая двумя точечными зарядами q₁ и q₂, (см. рис.2) равна

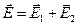. (1.9)

где 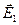– напряженность, создаваемая зарядом q₁ в точке А. 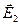– напряженность, создаваемая зарядом q₂ в точке А.

Модуль напряженности в случае суперпозиции двух полей

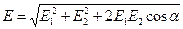, (1.10)

где α – угол между Е₁ и Е₂.

· Напряженность электростатического поля, создаваемого системой неподвижных точечных зарядов q₁, q₂, …, q_n:

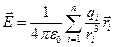, (1.11)

где 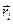– радиус-вектор, проведенный из точечного заряда 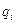в рассматриваемую точку поля, 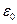– электрическая постоянная.

Энергетической характеристикой электрического поля является потенциал поля

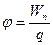, (1.12)

Потенциальная энергия поля точечного заряда

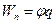. (1.13)

Потенциал электрического поля точечного заряда q на расстоянии r от него

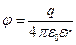. (1.14)

Потенциал поля металлической сферы радиусом R, несущей заряд q на расстоянии r от центра

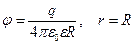; (1.15)

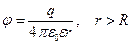. (1.16)

Связь напряженности и потенциала электрического поля

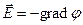, (1.17)

где gradφ – градиент потенциала.

Для сферической симметрии поля

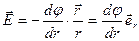. (1.18)