Примеры решения заданий для выполнения расчётно-графических работ
Пример 1.1 Электрическое поле создано бесконечной плоскостью, заряженной с поверхностной плотностью σ = 400 нКл/м2, и бесконечной прямой нитью, заряженной с линейной плотностью τ = 100 нКл/м. Нить расположена перпендикулярно плоскости. На расстоянии r = 10 см от нити находится точечный заряд q = 10 нКл. Определить силу, действующую на заряд.
| Дано: σ = 400 нКл/м2 τ =100 нКл/м r =10 cм q = 10 нКл | СИ 4·10-7 Кл/м2 0,1 м 10-8 Кл | Решение Модуль силы, действующей на заряд, помещенный в поле F = Eq, (1.19) здесь Е – модуль напряженности поля в точке, где находится заряд q. |
| F =? |
Согласно принципу суперпозиции электрических полей (1.9), напряженность поля, в точке, где находится заряд q:
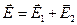 .
.
Поле, создаваемое плоскостью, однородно, и модуль напряженности в любой точке поля определяется по формуле:
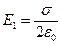 . (1.20)
. (1.20)
Поле заряженной линии неоднородно и модуль его напряженности определяется по формуле:
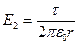 . (1.21)
. (1.21)
Так как векторы 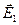 и
и 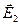 взаимно перпендикулярны, модуль результирующего вектора
взаимно перпендикулярны, модуль результирующего вектора 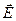 :
:
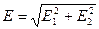 , (1.22)
, (1.22)
или
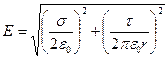 . (1.23)
. (1.23)
Используя формулу для силы ( ), получим
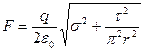 . (1.24)
. (1.24)
Проверка размерности
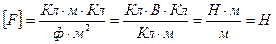 .
.
Вычисления
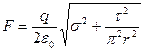 =
= 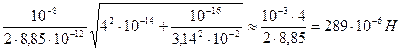 .
.
Ответ: сила, действующая на заряд, равна F = 289·10-6 Н.
Пример 1.2 В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды Q1 и Q2. Определить силу, действующую на заряд 1 нКл, помещенный в вершине треугольника. Угол при вершине 120°. Рассмотреть случаи:
1.Q1 = Q2 =2 нКл
2.Q1 = -2 нКл, Q2 =2 нКл
Дано: 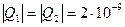 Кл;
Кл; 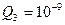 Кл; r = 0,08 м; a = 30°; e = 1, F1 и F2 -?.
Кл; r = 0,08 м; a = 30°; e = 1, F1 и F2 -?.
Решение
В соответствии с принципом суперпозиции поле каждого из зарядов Q1 и Q2 действует на заряд Q3 независимо. Это значит, что на заряд Q3 действуют силы, модули которых (рис.2)
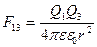 ,
, 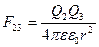 . (1.25)
. (1.25)
Так как 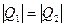 , то
, то 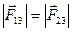 . Векторная сумма
. Векторная сумма 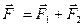 является искомой величиной. Модуль силы определяется:
является искомой величиной. Модуль силы определяется:
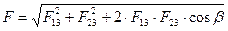 . В случае одноименных зарядов Q1 и Q2 из рис.3 видно, что угол b = 120°, поэтому
. В случае одноименных зарядов Q1 и Q2 из рис.3 видно, что угол b = 120°, поэтому 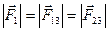 :
:
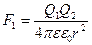 , (1.26)
, (1.26)
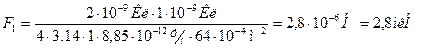
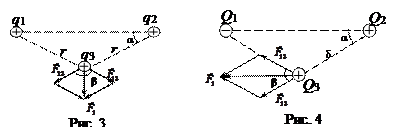
Случай разноименных зарядов Q1 и Q2 представлен на рис. 4. Видно, что угол b равен 60° и, следовательно,
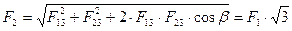 ;
;
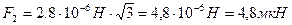 .
.
Ответ: силы, действующие на заряд в первом и во втором случаях: 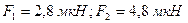 .
.
Дата добавления: 2016-07-22; просмотров: 3642;











