Примеры решения заданий для выполнения расчётно-графических работ

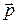Пример 2.1. Диполь с электрическим моментом р = 2 нКл∙м находится в однородном электрическом поле напряженностью Е = 30 кВ/м. Направление вектора составляет угол a = 60° с направлением линий напряженности электрического поля (рис.9, а).Определить:

1) момент сил, действующих на диполь;

2) произведенную ими работу при повороте диполя на угол b = 30°.

Решение

1. В соответствии с формулой (2.5) находим момент сил:

Его направление таково, что он стремится повернуть диполь в сторону совпадения направлений векторов 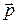и 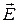(рис.9, а).Произведем вычисления:

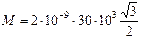Н∙м = 52∙10^-6 Н∙м

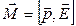,или М = рЕ sin a.

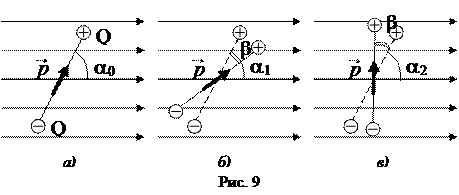
2. Из исходного положения (рис.9, б) диполь можно повернуть на угол b = 30° двумя способами: по часовой стрелке (рис.9, б)до угла a₁ = a - b= 30° или против часовой стрелки до угла a₂ = a + b = 90° (рис.9 в).

В первом случае диполь будет поворачиваться под действием механического момента сил поля, и работа этих сил положительная. Во втором случае поворот может быть осуществлен только под действием внешних сил, а механический момент сил поля препятствует этому повороту. Следовательно, работа сил поля при этом будет отрицательная.

Работу определим через изменение потенциальной энергии диполя в электрическом поле:

A = П₁- П₂.

Используя формулу (2.23), в первом случае можно записать

A₁ = – рЕ cos 60° + рЕ cos 30°,

а во втором

А₂ = – рЕ cos 60° + рЕ cos 90°.

Произведя вычисления, получим

А₁= 22,0 мкДж, А₂ = - 30,0 мкДж.

Ответ: момент сил, действующих на диполь 52∙10^-6 Н∙м, работа сил- 30,0 мкДж.

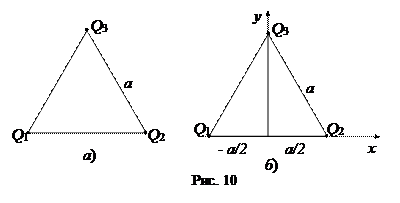
Пример 2.2.Три точечных заряда Q₁= 10 нКл, Q₂ = 10 нКл, Q₃ = −20 нКл расположены в вершинах правильного треугольника со стороной а = 10 см (рис. 10, а). Найти максимальное значение:

1) модуля напряженности электрического поля на расстоянии r₀ = 1 м от центра треугольника;

2) потенциала на расстоянии r₀ = 1 м от центра треугольника.

Решение

Выберем систему координат, как показано на рис. 10, б. Поле нейтральной системы зарядов на больших расстояниях от нее определяется ее дипольным моментом. Формулу (2.2) в проекциях на выбранные оси координат (с учетом, что х₃ = 0, у₁ = 0, у₂ = 0) запишем в виде

, .

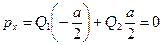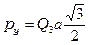Таким образом, электрический дипольный момент системы направлен вдоль оси 0у и, с учетом знака заряда, его проекция на эту ось равна

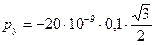Клּм = -17,3ּ10^–10 .Клּм.

В соответствии с формулами (2.3) и (2.4) максимальные значения модулей напряженности и потенциала при J₁ = 0 и J₂ = p, т.е. в точках, находящихся на оси 0у,равны

, .

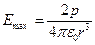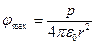Так как 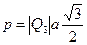, то

, .

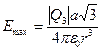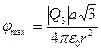После вычислений получим

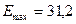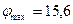В/м, В.

Ответ: максимальное значение модуля напряженности электрического поля 31,2 В/м, максимальное значение потенциала электрического поля 15,6 В.