Интерпретация моды, медианы и среднего
Если мы вынуждены выбрать одно число для замены любого из значений, то совпадение было бы максимальное число раз, если бы выбранное число было модой группы.
Если вместо каждого значения выбрать медиану, то достигается минимальная ошибка – при условии, что «ошибка» определяется как сумма абсолютного отличия каждого значения от оценки.
Если взамен каждого значения берется среднее, то обеспечивается минимальная ошибка – при условии, что «ошибка» определяется как сумма квадратов разностей каждого значения с оценкой.
Другие меры центральной тенденции
Среднее геометрическое n положительных чисел Х1, …, Хn определяется выражением
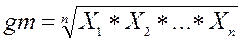 .
.
Гармоническое среднее n положительных значений Х1, …, Хn определяется выражением
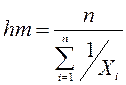 .
.
МЕРЫ ИЗМЕНЧИВОСТИ
Размах
Размах измеряет на числовой шкале расстояние, в пределах которого изменяются оценки. Разграничивают два его типа: включающий и исключающий.
Включающий размах – это разность между естественной верхней границей интервала, содержащего максимальное значение, и естественной нижней границей интервала, включающего минимальное значение.
Например, рост пяти мальчиков измеряют с точностью до ближайшего сантиметра. Получены следующие значения: 150, 155, 157, 165, 168 см. Фактический рост самого низкого мальчика находится где-то между 149,5 и 150,5 см и действительная нижняя граница равна 149,5 см. Верхняя граница интервала, содержащего максимальное значение, составляет 168,5 см. Таким образом, включающий размах равен разности 168,5 – 149,5 = 19.
Исключающий размах – это разность максимального и минимального значений в группе (168 – 150 = 18), что позволяет исключить возможное значение, находящееся выше максимального или ниже минимального.
В дальнейшем, если мы будем ссылаться на «размах» без указания, включающий он или исключающий, то выводы будут одинаково применимы для обоих.
Дисперсия
Для сравнения изменчивости двух совокупностей, которые отличаются по объему, используют меру изменчивости, называемую дисперсией
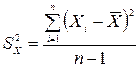 . (5.1)
. (5.1)
Иногда вычисления проще выполнить по формуле
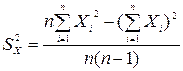 . (5.2)
. (5.2)
Если результат Хі повторяется с частотой fi, то дисперсию можно вычислить по формуле
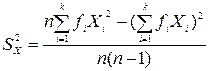 , (5.3)
, (5.3)
где k – количество разных значений, а 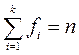 .
.
Дата добавления: 2020-10-01; просмотров: 626;











