Среднее, медиана и мода объединенных групп
Меры центральной тенденции. Меры изменчивости
МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
Мода
Мода (М0) – это такое значение во множестве наблюдений, которое встречается наиболее часто.
В совокупности значений (2, 6, 6, 8, 9, 9, 9, 10) модой является 9, потому что оно встречается чаще любого другого значения.
В случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа значений не имеет моды. Таким образом, в группе (1, 1, 3, 3, 6, 6) моды нет.
Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Итак, мода группы значений (0, 1, 1, 2, 2, 2, 3, 3, 3, 4, 5, 5) равна 2,5.
Если два несмежных значения в группе имеют равные частоты и они больше частот любого значения, то существуют две моды. В группе значений (10, 11, 11, 11, 12, 13, 14, 14, 14, 17) модами являются 11 и 14; в таком случае говорят, что группа оценок является бимодальной.
В больших множествах данных условились различать бóльшие и мéньшие моды (если частоты на двух вершинах не строго равны).
Наибольшей модой в группе называют единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколько меньших мод. Эти меньшие моды представляют собой локальные вершины распределения частот. Например, для группы значений (1, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9, 10, 10, 10, 10, 11, 11) наибольшая мода наблюдается при значении 6, а меньшие моды – при 3,5 и 10.
Медиана
Медиана, Md, представляет собой 50-й процентиль в группе данных. Это значение, которое делит упорядоченное множество данных пополам, так, что одна половина значений оказывается больше медианы, а другая – меньше.
Если данные содержат нечетное количество различных значений, например, 11, 13, 18, 19, 20, то медиана есть среднее значение для случая, когда они упорядочены, то есть Md = 18.
Если данные содержат четное число различных значений, например, 4, 9, 13, 14, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены: Md = (9 + 13)/2 = 11.
Если в данных есть объединенные классы, особенно в окрестностях медианы, то в таких случаях необходимо проводить интерполяцию внутри разряда значений.
Например, n = 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
Таблица 4.1
| Значение | Частота | Накопленная частота |
| 10,5 | ||
| 10,0 | ||
| 9,5 | ||
| 9,0 | ||
| 8,5 | ||
| 8,0 | ||
| 7,5 | ||
| 7,0 |
Оценкой медианы будет величина n/2 = 18-му значению снизу. Мы видим, однако, что 18-е значение лежит в интервале 8,25-8,75. Так как к нижней границе интервала накоплено 13 значений, нам надо пропустить еще 18-13 = 5 частот в интервале. А всего в интервале 9 частот, поэтому медиана лежит на 5/9 пути через интервал. Интервал содержит значения от 8,25 до 8,75, а его ширина равна 0,5; 5/9 этого расстояния – 0,28. Следовательно, медиана равна 8,25 + 0,28 = 8,53.
Нетрудно заметить, что Md = Р50, вычисленное по формуле (3.1)
Р50 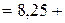
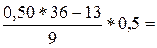
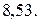
Среднее
Среднее совокупности n значений обозначается через 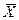 и определяется как
и определяется как
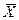
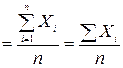 . (4.1)
. (4.1)
Среднее совокупности называют еще арифметическим средним или выборочным средним.
Если результат Хі повторяется с частотой fi, то среднее можно вычислить по формуле
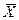
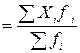 , (4.2)
, (4.2)
где суммирование осуществляют по всем интервалам.
Если задано групповое распределение частот, то для простоты допускают, что результаты равномерно распределены по каждому интервалу. При таком допущении частоту fi данных в любом интервале значений умножают на значение в середине интервала. Конечно, величина, которую вычисляют таким образом, только аппроксимация (то есть приблизительное значение) среднего несгруппированых данных. Для таблицы 3.1 (второй или третий столбец)
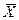
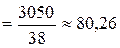 .
.
В результате аппроксимации (5 и 7 столбец) получаем
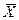
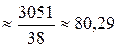 .
.
Среднее, медиана и мода объединенных групп
Мы можем знать средние, медианы и моды для трех разных классов школы и желать найти те же характеристики для объединения всех трех классов.
Пусть средние и количество учащихся для трех классов, А, В и С, будут:
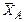 = 10,9 = 10,9
| 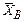 = 8,7 = 8,7
| 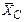 = 9,1 = 9,1
|
| nА = 24 | nВ = 30 | nС = 28 |
Среднее объединенной группы вычисляется по формуле, которая аналогична формуле (4.2):
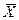
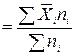 ,
,
которая дает 777,4/82 = 9,48.
Допустим, нам известно, что в другой группе А есть 6 значений (15, 15, 17, 17, 17, 18) и мода равна 17, а в группе В – 7 значений (14, 15, 15, 18, 19, 19, 19) и мода равна 19. Когда мы объединим А и В, оценка 15 попадется 4 раза и станет модой общей группы.
Чтобы определить и моду, и медиану необходимо иметь исходные данные.
Дата добавления: 2020-10-01; просмотров: 522;











