Дисперсия объединенных групп

Пусть a и b обозначают две различные группы:

	Группа a	Группа b
Объем группы	na	nb
Среднее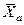
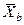
Дисперсия	Sa2	Sb2

Дисперсия группы n_a + n_b, образованной в результате соединения групп a и b, равна

S² = 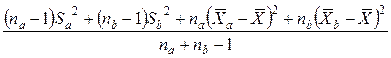, (5.4)

где .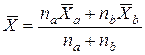

Стандартное отклонение S

Мерой изменчивости, тесно связанной с дисперсией, является стандартное отклонение. Стандартное отклонение, обозначаемое S, определяется как положительное значение квадратного корня из дисперсии. Для определения S надо сначала найти S², а затем вычислить из него квадратный корень

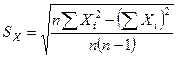. (5.5)

Асимметрия

Одно из наиболее важных свойств распределения частот – степень асимметрии. Практически точно симметричные полигоны частот и гистограммы почти никогда не встречаются. Степень асимметрии распределения частот для выборки называют просто его асимметрией. Легко выявить и распознать асимметрию, если рассматривать полигон частот или гистограмму, но это не всегда возможно или удобно. Поэтому изобретены различные обобщенные статистические характеристики, оценивающие вид и степень асимметрии группы наблюдений.

Наилучшая мера асимметрии для группы данных выражается формулой

As = 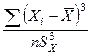. (5.6)

Поскольку вычисление по формуле (5.6) очень утомительно, то для умеренно больших выборок (n = 50 и более) можно проводить вычисления по формуле

As = 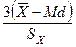, (5.7)

т. е. асимметрия распределения равна отношению утроенной разности среднего и медианы к стандартному отклонению. Асимметрия из уравнения (5.7) может принимать значения в диапазоне от –3 до +3.

Если As > 0 (As < 0), то говорят, что распределение имеет положительную (отрицательную) асимметрию. При этом в унимодальных положительно (отрицательно) асимметричных распределениях среднее больше (меньше) медианы, которая в свою очередь больше (меньше) моды.

В симметричном распределении As = 0.

Эксцесс

Эксцесс – греческое слово, обозначающее свойство «остроконечности» кривой. Понятие «эксцесс» применимо лишь к унимодальным распределениям и относится к крутизне кривой в окрестности единственной моды. (Если распределение имеет две моды, то принято говорить об эксцессе кривой в окрестности каждой моды.)

Обычная мера эксцесса определяется следующей формулой

Эксцесс = 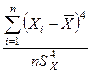. (5.8)

Соотношения между величиной статистики эксцесса и «островершинностью» распределения, для которого она вычислялась, показаны в таблице 5.1.

Таблица 5.1 – Соотношение величины статистики эксцесса с «островершинностью» распределения частот

Характер распределения	Описание «островершин-ности»	График	Величина статистики эксцесса
Плоское	Плосковершинное		Менее 3 (должна быть не меньше нуля)
Островершинное	Островершинное		Больше 3 (может быть очень большой)
Нормальное	Средневершинное

Нормальное распределение рассматривается в следующей лекции.