Критерий гарантированного результата

Его также называют максимшшым критерием Вальда. Сущность данного критерия заключается в следующем. ЛПР располагает множе­ством стратегий (вариантов, альтернатив) решения проблемы:

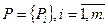
Указанные стратегии считаются контролируемыми (управляемыми) факторами. Наряду с факторами управляемыми действуют факторы, которые не поддаются контролю. Обозначим их

через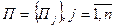

В качестве 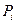могут быть технические параметры проектируемых сис­тем экономические показатели состояния предприятия, различные варианты решения поставленных задач и т.п

Факторы 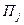представляют: уровень спроса на товары, предла­гаемые фирмой, рыночные цены, условия эксплуатации техничес­ких и произ­водственных систем, действия конкурентов и т.д.

Для оценки эффективности принимаемых решений вводим показа­тель эффективности Е и считаем, что функция Е(Р, П) яв­ляется извест­ной. Так как факторы Р и П являются дискретными, то и эффектив­ность Е также представляет собой множество диск­ретных чисел. Таким образом, каждой точке контролируемых и неконтролируемых факто­ров ( 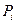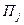)ставится в соответствие зна­чение эффективности Е (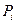 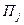). Следовательно, можно построить матрицу 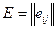, которая представ­лена в виде табл. 5.1.

Т а б л и ц а 5.1

Матрица эффективности

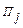
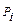
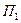
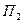
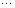
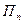
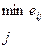
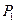
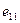
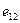
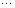
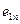
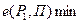
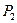
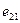
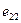
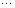
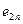
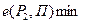
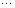
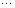
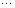
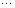
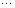
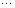
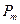
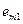
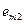
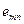
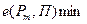
Для каждого контролируемого фактора 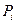(строки) нахо­дится 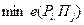, в результате чего определяется набор значений показателя эффективности 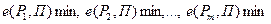. Сравнивая полученные величины, выбирают управляемый фак­тор 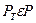, при котором, обеспечивается максимальное значе­ние Е(Р, П).

Таким образом, критерий гарантированного результата (максимин­ный критерий Вальда) записывается в виде

E(P,П) = max min e_ij (7)

обеспечивает максимизацию минимально го выигрыша или, что-то же самое, минимизацию максимальных потерь, которые могут быть при реализации одной из стратегий. Критерий прост и четок, но кон­сервативен в том смысле, что ори­ентирует принимающего решение на слишком осторожную линию поведения. Величина, соответствующая максимальному критерию, называется нижней ценой игры, под кото­рой следует понимать максимальный выигрыш, гарантируемый в игре с данным про­тивником выбором одной из своих стратегий при мини­мальных результатах. Это перестраховочная позиция крайнего песси­миз­ма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хо­чет себя застраховать от неожиданных проигрышей. Выбор такой стра­тегии определяется отношением игрока к риску.

Рассмотрим следующую задачу. Пусть, например, предприя­тие гото­вится к переходу на новые виды продукции, при этом воз­можны че­тыре решения 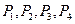, каждому из которых соот­ветствует определен­ный вид выпуска или их сочетание.

Результаты принятия решений существенно зависят от обста­новки, которая в значительной мере неопределенна. Варианты обстановки ха­рактеризует структура спроса на новую продукцию, которая может быть трех типов: .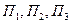

Выигрыш, характеризующий относительную величину резуль­тата (доходы, прибыль и т.п.), соответствующий каждой паре со­четаний решений Р и обстановки П, представлен в табл. 5.2.

Нужно найти такую стратегию (линию поведения) 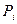, которая по сравнению с другими является наиболее выгодной (оптимальной). По­казатель эффективности

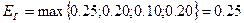
и, следовательно, предпочтение необходимо отдать варианту .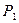

Выбрав решение 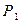, мы независимо от вариантов обстановки полу­чим выигрыш не менее 0,25. При любом другом решении, в случае не­благоприятной обстановки, может быть получен результат (выигрыш) меньше 0,25.

Таблица 5.2

Эффективность выпуска новых видов продукции

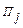
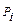
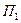
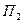
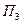
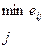
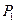
	0,25	0,35	0,40	0,25
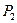
	0,75	0,20	0,30	0,20
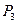
	0,35	0,80	0,10	0,10
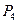
	0,90	0,20	0,30	0,20

Так, при выборе решений 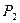, полу­ченный выигрыш, в зависимости от наступившего варианта об­становки, будет колебаться от 0,2 до 0,75. Для решений 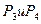границы, в которых будет колебаться выигрыш, составят 0,10:0,80 и 0,20:0,90.

Отметим еще раз, что этот критерий ориентирует ЛПР на слишком осторожную линию поведения. Так этот критерий ни­как не учитывает, что в случае принятия решения 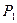(т.е. при ори­ентации на выигрыш 0,25), максимальный выигрыш не превыша­ет 0,4. В то время, как вы­бирая, например, решение 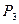при гаран­тированном выигрыше 0,1 в слу­чае благоприятной обстановки можно получить выигрыш равный 0,80.

В ряде экономических задач в качестве критерия эффективно­сти принимаемых решений выступает показатель минимума зат­рат. В этих ситуациях принцип гарантированных затрат форму­лируется в виде

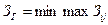(8)

В качестве затрат 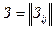могут выступать: капитальные вло­жения, валовые издержки производства, приведенные годовые затраты и дру­гие показатели.

Пример. Производится сравнение различных инвестиционных про­ектов 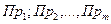. Для реализации каждого из проектов необхо­дима определенная величина капитальных вложений

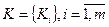, величины 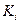,являются управляющими (контроли­руемыми) факторами.

Каждому проекту соответствует определенное значение себес­тоимо­сти продукции, которую предполагается выпускать при ре­ализации проекта. Совокупность значений себестоимости продук­ции представ­ляется в виде:

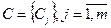
Величины 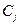на начальных этапах выполнения проекта точно опреде­лить невозможно, поэтому они считаются неконтролируе­мыми факторами. Каждой паре 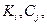соответствует опреде­ленное значение приведенных годовых затрат, определяемых по формуле

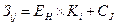
где 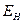— нормативный коэффициент эффективности капитальных вложе­ний.

Располагая наборами 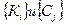, составляем матрицу приве­денных за­трат 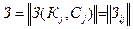которая приведена в табл. 5.3.

Таблица 5.3

Зависимость приведенных затрат от К и С

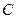
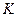
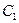
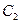
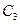
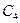
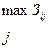
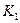
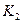
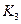
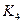
Критерий гарантированных затрат реализуется как

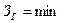{130,200,200; 150}= 130.

В качестве наиболее эффективной выступает первая стратегия, кото­рой соответствуют капитальные вложения 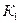[13].

Критерий оптимизма

При использовании данного критерия, называемого также кри­терием максимакса, ЛПР ориентируется на то, что условия функционирования анализируемых систем будут для него наиболее бла­гоприятными. Вследствие этого оптимальным решением является стратегия, приво­дящая к получению наибольшего значения критерия оптимальности в платежной матрице. Этот критерий целесообразно применять в тех случаях, когда имеется принципиальная возможность повлиять на функции противоположной стороны.

Если анализируется матрица эффекта Е(Р, П) того или иного вида, то выбор управляемых факторов осуществляется таким об­разом, чтобы обеспечить максимум эффекта. И в этом случае кри­терий оптимизма записывается в виде

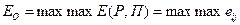
Пример. Анализируется матрица выпуска новых видов продукции, приведенная в табл. 5.2. Необходимо определить оптимальную страте­гию с помощью принципа оптимизма. В данном случае принцип опти­мизма записывается в виде

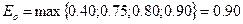
что отвечает выбору решения .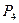

Если рассматривается матрица затрат, то управляемые факторы вы­бираются так, чтобы минимизировать указанные затраты. Тогда рас­сматриваемый критерий формируется следующим образом:

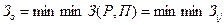
Пример. Рассматривается матрица приведенных годовых зат­рат, со­ответствующая табл. 2.3. Необходимо определить наибо­лее эффектив­ную стратегию, используя критерий оптимизма. Применительно к рас­сматриваемой ситуации принцип оптимизма может быть представлен в виде

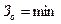{75,80,60,90}= 60.

Следовательно, наиболее эффективной является стратегия, соот­вет­ствующая 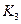. Сравнивая два данных решения этого пункта и решения, полученные при использовании критерия гарантирован­ных затрат, ви­дим, что они не совпадают. Следует ожидать, что такая ситуация будет характерна для большинства анализируемых реальных задач из-за принципиальных отличий критериев. Отметим, что ситуации, требую­щие применения критерия оп­тимизма, в экономике в общем нередки и пользуются им не только безоглядные оптимисты,, но и игроки, по­ставленные в безвы­ходное положение, когда они вынуждены руково­дствоваться прин­ципом «или пан, или пропал».