Понятие игры с природой

Почему стратегия, риска является исключительно современным по­нятием? Почему должны были пройти тысячелетия, прежде чем доб­равшееся до Ренессанса человечество смогло пробиться через барьеры, стоящие на пути измерения риска и контроля над ним? Ответить на этот вопрос нелегко. Мы начнем с главного. С самого начала писаной истории игра, эта квинтэссенция риска, была популярным развлече­нием, а частенько и пагубным пристра­стием многих людей. Именно загадки азартной игры, а не глобальные вопросы о природе капита­лизма или проникновении в тайны грядущего подвигли Паскаля и Ферма па революционный прорыв в сферу вероятностных закономер­ностей. До этого момента на протяжении всей истории люди заклю­чали пари и играли в азартные игры, не используя известной нам сис­темы оценки шансов выигрыша или проигрыша. Выбор стратегии игры носил исключительно интуитивный характер и не направлялся ника­кими предписаниями теории.

В игре человек всегда склонен к безрассудству, поскольку она ставит его лицом к лицу с судьбой, никому не открывающей сво­их намерений. Мы ввязываемся в эту бескомпромиссную битву, потому что верим, что у нас есть могучий союзник — госпожа Удача, которая непременно вмешается в наши отношения с судь­бой и принесет победу. Адам Смит, тонкий знаток человеческой природы, определял мотивацию иг­рока как «свойственную боль­шинству людей самонадеянную пере­оценку своих способностей и абсурдную веру в свою счастливую звезду». Следует отметить, что Смит, хотя и отдавал себе отчет в том, что человеческая предрасположенность к риску способствует экономи­ческому прогрессу, высказал опасение, что общество может постра­дать, если эта склонность перейдет разумные границы. Поэтому он ос­торожно балансировал на грани морализирующих предостережений касательно пользы свободного рынка. Спустя сто шестьдесят лет ему вторил другой великий английский экономист Джон Мейиард Кейнс: «Если основой развития страны становится прибыль от казино, пиши - пропало».

Однако жизнь была бы скучна, если бы людям недоставало смелости и веры в свою звезду. Кейнс допускал, что «если бы человеку по его природе не свойственно было искушение испытать свой шанс то на долю одного лишь холодного расчета пришлось бы не так уж много инвестиций». Никто не рискует в ожидании проигрыша.

Игра приковывала к себе человечество в течение тысячелетий, Она завлекала всех — и отбросы общества, и наиболее респектабельные его слои.

Достаточно часто решения приходится принимать в условиях неоп­ределенности, то есть в таких условиях, когда или процесс выполнения операции является неопределенным, или нам сознательно противодей­ствует противник, или нет ясных и четких целей операции.

Наличие неопределенностей значительно усложняет процесс выбора эффективных (оптимальных) решений и может привести к непредска­зуемым результатам. На практике, при проведении экономического анализа, во многих случаях пытаются не замечать указанное «зло», вы­званное фактором неопределенности, и действуют (принимают реше­ние) на основе детерминированных моделей. Иначе говоря, предпола­гается, что факторы, влияющие на принимаемые решения, известны точно. К сожалению, действительность часто не соответствует таким представлениям. Поэтому политика выбора эффективных решений без учета неконтролируемых факторов во многих случаях приводит к зна­чительным потерям экономического, социального и иного содержания.

Рассматривая неопределенность, которая является наиболее харак­терной причиной риска в экономической деятельности, необходимо отметить, что выделение и изучение ее применительно к процессу эко­номической, управленческой, финансовой и других видов деятельности является крайне необходимым, поскольку при этом отображается прак­тическая ситуация, когда нет возможности осуществлять перечислен­ные виды деятельности в условиях, которые не могут быть однозначно определены.

В целом ряде экономических задач приходится анализировать си­туации, в которых необходимо принимать решения в условиях неопре­деленности, то есть, например, возникают ситуации, в которых сталки­ваются интересы двух или более конкурирующих сторон, каждая из которых преследует свою цель, причем результат любого мероприятия каждой из сторон зависит от того, какие действия предпримет против­ник. Это особенно характерно в ус­ловиях рыночной экономики. Такие ситуации называют конфликтными. Научно обоснованные методы ре­шения задач с конфликтными ситуациями дает теория игр.

Теория игр — это теория математических моделей принятия опти­мальных решений в условиях неопределенности, противоположных интересов различных сторон конфликта. Матричные игры могут слу­жить математическими моделями многих простейших конфликтных ситуаций из области экономики. В частности, тео­рия игр применяется в вопросах борьбы фирм за рынки, в явлениях олигополии, в планирова­нии рекламных компаний, при формировании цен на конкурентных рынках, в обменных и торговых операциях, в биржевой игре, в анализе коалиционного поведения и т.д. С позиций теории игр можно рассмат­ривать вопросы централизации и децентрализации управления произ­водством, оптимальное планирование по нескольким показателям, планирование в условиях неопределенности, порождаемой, например, техническим прогрессом, преодоление ведомственных противоречий и другие вопросы.

Как уже отмечалось, теория игр — это теория математических моде­лей принятия оптимальных решений в условиях конфликта или неоп­ределенности. При этом конфликт не обязательно должен быть антаго­нистическим, в качестве конфликта можно рассматривать любое разно­гласие.

Рассмотрим следующий экономический пример. Пусть требуется принять решение о выпуске на рынок некоторого товара. Может слу­читься, что объем спроса на этот товар известен точно; может быть, что известно лишь статистическое распределение возможных значений спроса; наконец, может оказаться, что известны лишь границы, в кото­рых заключен спрос, но никаких даже вероятностных соображений о его предстоящих значениях нет. Последний случай квалифицируется как неопределенность. Такая неопределенность может возникнуть, ко­гда спрос (например, на сезонные товары) зависит от метеорологиче­ских условий (конфликт с природой) или, в условиях рынка, от дея­тельности конкурента, уже удовлетворившего неизвестную часть спроса. Приведенные примеры при определенных условиях могут быть приве­дены к игре.

Всякая теоретико-игровая модель должна отражать, кто и как кон­фликтует, а также, кто и в какой форме заинтересован в том или ином исходе конфликта.

Действующие в конфликте стороны будем называть игрока­ми, а ре­шения, которые способны принимать игроки, — стратегиями.

Содержание математической теории игр состоит, во-первых, в уста­новлении принципов оптимального поведения игроков в играх, во-вто­рых, в доказательстве существования ситуаций, которые складываются в результате применения этих принципов, и, в-третьих, в разработке методов фактического нахождения таких ситуаций. [13]

Предмет теории игр. Основные понятия

Теория игр является теорией математических моделей принятия ре­шений в условиях конфликтов. Здесь под конфликтом будем понимать явление, применительно к которому можно говорить, кто и как в этом явлении участвует, какие у него могут быть исходы и кто и как в этих исходах заинтересован. Поэтому для формального задания конфликта необходимо указать:

1) множество участвующих в нем действующих начал, называемых коалициями действия;

2) семейство множеств стратегий каждой из коалиций действия;

3) множество ситуаций;

4) множество заинтересованных начал, называемых коалициями ин­тересов;

5) семейства отношений, выражающих предпочтения между ситуа­циями для коалиций интересов.

Перечисленная система множеств и называется игрой. Содержание теории игр состоит в установлении связей между компонентами каж­дой игры и оптимальными ее исходами, и прежде всего, в уточнении самого понятия оптимальности, в доказательстве существования опти­мальных исходов и в их фактическом определении.

Дли игр с. одной коалицией действия множество всех ситуаций можно принять за множество стратегий этой единственной коалиции действия и далее о стратегиях не упоминать. Поэтому такие игры назы­ваются нестратегическими. Важным классом таких игр являются игры с природой, применяемые для анализа экономических ситуаций, оценки эффективности принимаемых решений и выбора наиболее предпочтительных альтернатив, в которых риск связан с совокупно­стью неопределенных факторов окружающей среды, именуемых «при­рода». Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя вполне могут встречаться ситуации, в которых игроком действительно может выступать природа (например, обстоятельства, связанные с по­годными условиями или с природными стихийными силами).

В отличии от нестратегических игр, все остальные игры, с двумя или более коалициями действия, называются стратегическими. В практиче­ских ситуациях часто появляется необходимость

согласования действий компаний, объединений, министерств и дру­гих участников проектов в случаях, когда их интересы не совпадают. В подобных ситуациях теория стратегических игр позволяет найти опти­мальное решение для поведения всех участников проекта, обязанных согласовывать действия при столкновении интересов.

Риск и неопределенность исходов игры обусловливаются случайным состоянием среды или выбором образа действия противоположной стороной, или вероятностным характером появления желаемого ре­зультата по возможным стратегиям.

В этой главе рассматриваются различные экономические ситуации, в которых риск связан с совокупностью неопределенных факторов ок­ружающей среды, именуемых «природа».

В играх с природой, как и в стратегических играх, создание модели должно начинаться с построения платежной матрицы. Это наиболее трудоемкий и ответственный этап подготовки принятия решения, так как ошибки в платежной матрице не могут быть компенсированы ни­какими вычислительными методами и могут привести к неверному итоговому результату.

Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком 1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре.

Методы принятия решений в играх с природой зависят от того, известны или нет вероятности состояний (стратегий) природы, т.е. имеет ли место ситуация риска или неопределенности.

Предположим, что построена следующая платежная матрица игры с природой:

(5)

Здесь игрок 1 имеет т возможных ситуаций 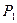, ,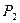…, , 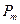а у при­роды имеется n возможных состояний (стратегий) , , ... , .

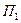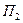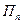Платит, естественно, не природа, а некая третья сторона (или сово­купность сторон, влияющих на принятие решений игроком 1 и объеди­ненных в понятие «природа»).

Можно задавать матрицу игры с природой и в виде так называемой матрицы рисков 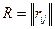или матрицы упущенных возможностей. Вели­чина риска — это размер платы за отсутствие информации о со­стоянии среды. Матрицу R строим на основе матрицы

выигрышей .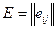

Риском 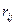.игрока при использовании им стратегии 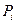, и при состоя­нии среды 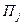будем называть разность между выигрышем, который игрок. Получил бы , если бы он знал, что состоянием среды будет 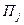, выигрышем который игрок получит, не имея этой информации.

Зная состояние природы (стратегию) 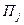игрок выбирает ту страте­гию, при которой его выигрыш максимальный, т.е.

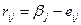(6)

где 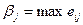при заданном j.

Независимо от вида матрицы игры требуется выбрать такую стратегию игрока, которая была бы наиболее выгодной по сравнению с другими.