Измерение характеристик случайных процессов

Если случайный процесс является эргодическим, то его реализация достаточной длины есть «типичный» представитель статистического ансамбля. Изучая эту реализацию экспериментально, можно получить много сведений, характеризующих данный случайный процесс.

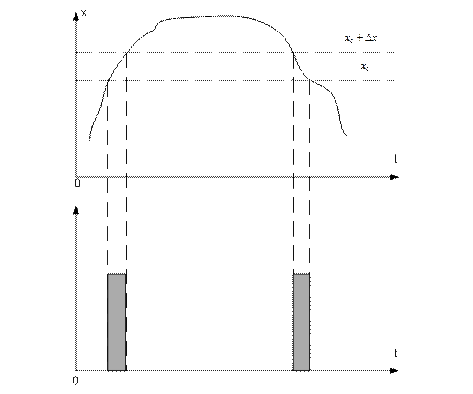
Прибор для измерения одномерной плотности вероятности случайного процесса может быть выполнен следующим образом. Одномерная плотность вероятности эргодического случайного процесса есть величина пропорциональная относительному времени пребывания его реализации на уровне между x и 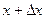. Предположим, что имеется устройство с двумя входами, на один из которых подаётся исследуемая реализация x(t), а на другой опорное напряжение, уровень которого можно регулировать. На выходе устройства возникают прямоугольные видеоимпульсы постоянной амплитуды, начало и конец которых определяется моментами времени, когда текущие значения случайного сигнала совпадают либо с уровнем 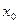либо с уровнем 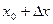. Если теперь измерить, скажем, с помощью обычного стрелочного прибора среднее значение тока, создаваемого последовательностью видеоимпульсов, то показания прибора будут пропорциональны плотности вероятности .

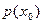Любой достаточно инерционный стрелочный прибор может быть использован для измерения математического ожидания случайного процесса (смотри формулу 6.5).

Прибор, измеряющий дисперсию случайного процесса, как это следует из (6.6) , должен иметь на входе конденсатор, отделяющий постоянную составляющую. Дальнейшие этапы процесса измерения – возведение в квадрат и усреднение по времени – выполняются инерционным квадратичным вольтметром.

Принцип работы измерителя функции корреляции (коррелометра) вытекает из формулы (6.7). Здесь мгновенные значения случайного сигнала после фильтрации постоянной составляющей, разделяясь на два канала поступают на перемножитель, причём в одном из каналов сигнал задерживается на время 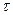. Для получения значения функции корреляции сигнал с выхода перемножителя обрабатывается инерционным звеном, которое осуществляет усреднение.