Характеристики случайных процессов

Определим в начале основные характеристики случайных величин. Пусть Х – случайная величина, т.е. совокупность всевозможных вещественных чисел x, принимающих случайное значение. Исчерпывающее описание статистических свойств Х можно получить, располагая неслучайной функцией F(x) вещественного аргумента x, которая равна вероятности того, что случайное число из X примет значение, равное или меньшое конкретного х:

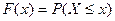(6.1)

Функция F(x) называется функцией распределения случайной величины Х. Если Х может принимать любые значения, то F(x) является гладкой неубывающей функцией, значения которой лежат на отрезке 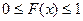. Имеют место следующие предельные равенства: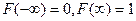

Производная от функции распределения 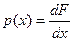есть плотность распределения вероятности (или, короче плотность вероятности) данной случайной величины.

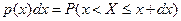(6.2)

То есть величина 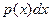есть вероятность попадания случайной величины Х в интервал .

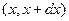Для непрерывной случайной величины Х плотность вероятности р(x) представляет собой гладкую функцию. Если же Х – дискретная случайная величина, принимающая фиксированные значения 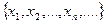с вероятностями 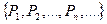соответственно, то для неё плотность вероятности выражается как сумма дельта-функций.

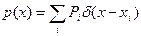(6.3)

В обоих случаях плотность вероятности должна быть неотрицательной: 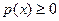и удовлетворять условию нормировки:

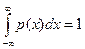(6.4)

Рассмотрим теперь плотность вероятности для случайных процессов. Пусть Х(t) случайный процесс, заданный ансамблем реализаций а 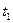- некоторый произвольный момент времени. Фиксируя величины 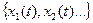, получаемые в отдельных реализациях, осуществляем одномерное сечение данного случайного процесса и наблюдаем случайную величину 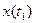. Её плотность вероятности 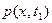называется одномерной плотностью вероятности процесса X(t) в момент времени .

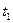Информация которую можно извлечь из одномерной плотности вероятности, недостаточна для того, чтобы судить о характере развития реализаций случайного процесса во времени. Гораздо больше сведений можно получить, располагая двумя сечениями случайного процесса в несовпадающие моменты времен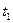и и .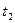

Возникающая при таком мысленном эксперименте двумерная случайная величина 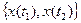описывается двумерной плотностью вероятности .

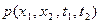Естественным обобщением является n-мерное сечение случайного процесса (n>2), приводящее к n-мерной плотности вероятности .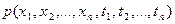

Многомерная плотность вероятности случайного процесса должна удовлетворять обычным условиям, налагаемым на плотность вероятности совокупности случайных величин. Помимо этого, величина 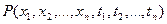не должна зависеть от того, в каком порядке располагаются её аргументы (условие симметрии).