Типовые модели случайных сигналов

А) Белый шум.

стационарный случайный процесс с постоянной на всех частотах спектральной плотностью мощности называется белым шумом.

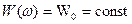(6.34)

Термин «белый шум» образно подчёркивает аналогию с «белым» (естественным) светом, у которого в пределах видимого диапазона интенсивность всех спектральных составляющих приблизительно одинакова.

По теореме Винера-Хинчина функция корреляции белого шума:

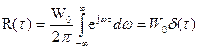равна нулю всюду кроме точки 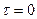. Средняя мощность (дисперсия) белого шума неограниченно велика.

Белый шум является дельта-коррелированным процессом. Некоррелированность мгновенных значений такого случайного сигнала означает бесконечно большую скорость изменения их во времени – как бы мал ни был интервал 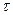, сигнал за это время может измениться на любую наперёд заданную величину.

Белый шум является абстрактной математической моделью и отвечающий ему физический процесс в природе, безусловно, не существует. Однако это не мешает приближённо заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал, оказывается существенно уже эффективной ширины спектра шума.

Б) Случайный синхронный телеграфный сигнал

Найдём функцию корреляции и спектральную плотность мощности телеграфного сигнала. Под случайным синхронным телеграфным сигналом понимается центрированный случайный процесс, принимающий с равной вероятностью значения +1 и -1, причём смена значения может происходить только в моменты времени, разделённые промежутком 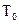(тактовым интервалом). Значения на разных тактовых интервалах независимы. Пример реализации такого процесса приведен на рисунке:

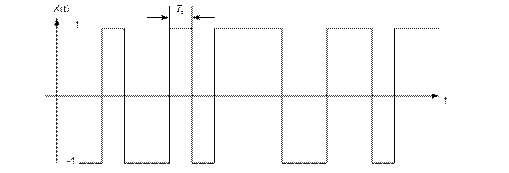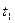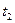Границы тактовых интервалов у разных реализаций не совпадают, так что любой момент времени на интервале от 0 до Т может с равной вероятностью оказаться моментом начала такта. Для определения функции корреляции рассмотрим два сечения в моменты и , обозначим 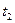- 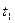через 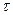и найдём математическое ожидание произведения 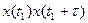. Если 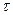> 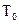, то эти сечения принадлежат разным тактовым интервалам, и произведение может с равной вероятностью принимать значения +1 и -1, так что его математическое ожидание равно нулю. Если же 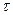< 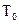, то возможны два случая: случай А, когда они принадлежат одному интервалу и следовательно, 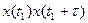=1, и случай Б, когда они принадлежат разным интервалам и 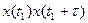может с равной вероятностью равняться +1 и -1. Поэтому при 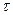< 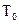математическое ожидание 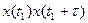равно вероятности P(A) того, что оба сечения оказались в одном интервале. Отсюда видно что случай А имеет место, если первое из двух сечений отстоит от начала тактового интервала не более чем на 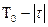, а вероятность этого равна 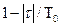. Таким образом:

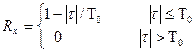
Так как 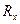зависит только от разности 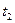- 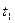= 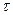, а 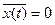, то процесс стационарный.

График функции корреляции

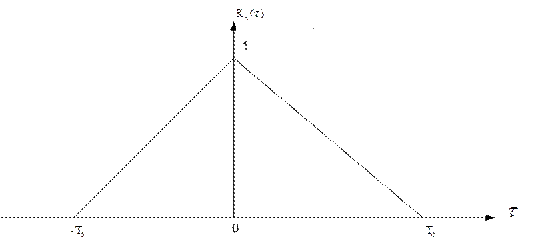Спектральную плотность мощности синхронного сигнала можно определить по формуле

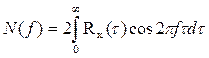
Откуда:

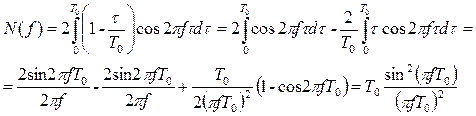(6.35)

График спектральной плотности:

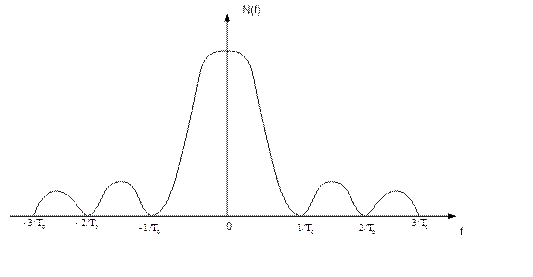
В) Гауссово (нормальное) распределение.

В теории случайных сигналов фундаментальное значение имеет гауссова плотность вероятности.

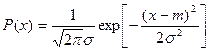(6.36)

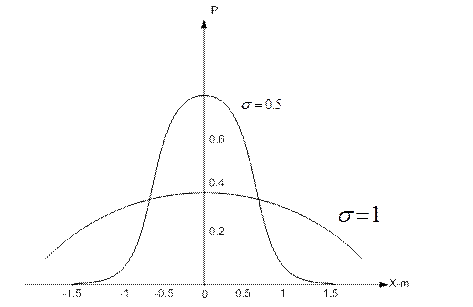
содержащая два числовых параметра m и 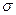. График данной функции представляет собой колоколообразную кривую с единственным максимумом в точке x=m. При уменьшении 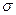график всё более локализуется в окрестности точки x=m.

Непосредственным вычислением можно убедиться, что параметры гауссова распределения имеют смысл соответственно математического ожидания и дисперсии: 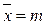; 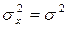. Функция распределения гауссовой случайной величины

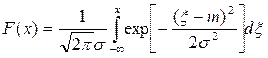
Замена переменной 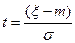даёт:

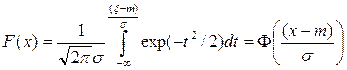(6.37)

Здесь Ф интеграл вероятностей

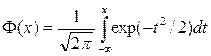
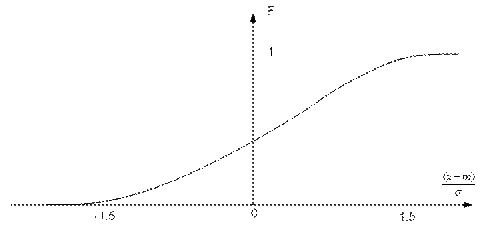
График функции F(x) имеет вид монотонной кривой, изменяющейся от 0 до 1.