Атака на основе невыполнимых дифференциалов

Square атака

Square атака первоначально была представлена как специализированная атака на блочный шифр Square [59]. Она осуществляется путем исследования пословной структуры шифра, где все блоки данных расщепляются и обрабатываются в виде 8-битовых слов. Эта атака была также применена к другим блочным шифрам со структурой Фейстеля или SPN, таким как IDEA [167], Skipjack [173, 95], MISTY1 [111] и SAFER [119]. Атака тесно связана с атаками насыщения, предложенными Люком [143], интегральным криптоанализом Хью и др. [94] и структурным криптоанализом Бирюкова и Шамира [32]. Square атака – это атака с выбранными открытыми текстами, которая имеет сходство с дифференциальными атаками высокого порядка [119] в том смысле, что при выполнении этой атаки используют повторяющуюся разность (повторение разности) нескольких слов, связанных некоторой групповой операцией как инвариантное свойство, выполняющееся для множества циклов шифра. Это аналогично случаю, когда пара текстов с разностным оператором, используемым как распознаватель в дифференциальном криптоанализе (DC). Тем не менее, в [125] Кнудсен и Вагнер переименовали свой метод в метод интегрального криптоанализа, формулируя его в виде схемы, отличной от дифференциалов высокого порядка.

Базовые инструменты в Square атаке связаны с понятиями состояния слова, мультимножества и интегралами.

Определение 2. Мультимножество из e элементов определяется как функция .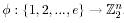

Определение 3. Говорят, что n-битовое мультимножество из k×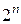элементов активно, если любое значение из Z 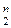появляется точно k раз.

Определение 4. Говорят, что n-битовое мультимножество пассивно, если оно принимает фиксированное значение .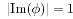

Определение 5. Говорят, что n-битовое мультимножество является искаженным, если оно не активно не пассивно.

Определение 6. Состояние слова может быть активным пассивным или искаженным.

Следующее определение обобщает первоначальную концепцию, представленную в исходной работе [59]:

Определение 7. ( 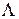-множество) 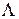-множеством называется мульти-множество из 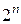текстовых блоков, в котором n-битовые слова являются активными, пассивными или искаженными.

Определение 8. (Сбалансированные слова в 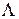-множестве) Пусть 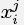будет j-м значением n-битного слова x_i на i-й позиции 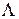-множества. Всякий раз, когда значение интеграла

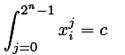
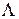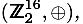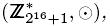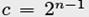поддерживается для заданной константы c, слово x_i считается сбалансированным над заданным -множеством. Интегральная операция и константа c зависят от групповой операции, например, c = 0 для или c = 0 для или для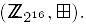

Выражение «интеграл по сумме слов» в 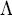-множестве заимствовано из работы Кнудсена и Вагнера [125]. Тем не менее, их определение расширяет понятие для суммы переменных на произведения переменных, в зависимости от используемой в шифре групповой операции. Наиболее часто при построении Square атаки используют оператор Исключающее ИЛИ (XOR). Это решение базируется на факте, что активные, пассивные, сбалансированные и искаженные (несбалансированные) слова можно более точно различить с помощью XOR операции. Для оператора умножения 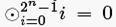для активного слова,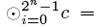 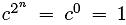для пассивного слова, но для сбалансированного слова произведение может принимать любое значение. Для оператора сложения 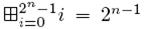для активного слова, для пассивного слова, но сумма сбалансированных слов может принимать любое значение.

Активные и пассивные слова по определению всегда являются сбалансированными. Искаженные слова также могут быть сбалансированными, но не всегда.

Square атака начинается путем тщательного выбора 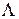-множества так, чтобы, по меньшей мере, одно сбалансированное слово можно было идентифицировать вдоль цепочки 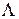-множеств для максимально возможного числа циклов в шифре. Путем слежения за распространением сбалансированных слов через множество циклов можно идентифицировать комбинацию активных, пассивных и искаженных слов. Такая комбинация полезна для атаки пока
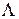-множество содержит, по меньшей мере, одно сбалансированное слово. Эта цепочка 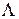-множеств, вместе с интегралом, может использоваться как распознаватель случайной перестановки или в атаке с восстановлением ключа для определения подключей в циклах, окружающих цепочку. В зависимости от числа анализируемых циклов Square атака может быть классифицирована следующим образом:

Определение 9.(tR-атака) tR Square атакой на n-цикловый шифр называется атака с восстановлением ключа, которая использует интегральное свойство для восстановления битов подключа с помощью (n-t)-цикловой цепи
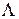-множеств.

Значение t может быть дробным, если только часть цикла включена в атаку, такую как линейные атаки.

В [125] Кнудсен и Вагнер дали понятие интегралов высокого порядка, как соответствующие мультимножества с большим размером слов. Предположим, шифр действует на блоке из n-битовых слов. Интеграл высокого порядка для такого шифра будет использовать мультимножества с n-битными (активными, пассивными или искаженными) словами. Интеграл второго порядка будет использовать 2n-битовые слова. Определение естественно расширяется до высоких порядков. Однако количество выбранных открытых текстов резко возрастает с увеличением порядка интеграла. Примером S мультимножества 1-го порядка c словами является

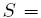
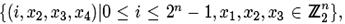и

Примером мультимножества 2-го порядка является

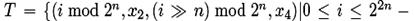
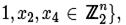
где >> означает сдвиг вправо на n битов, 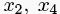– фиксированные n-битовые слова, и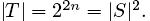

Атака на основе невыполнимых дифференциалов

В этом разделе дается описание метода, который основан на работах Борца и др. [43], Бихам и др.. [18] и Кнудсена [116]. В обычной DC атаке с целью отличия шифра от случайной перестановки находятся характеристики высоковероятных дифференциалов для осуществления, в конечном счете, атаки с восстановлением ключа. В таких атаках биты подключа угадываются в циклах, окружающих дифференциал. Подключи, которые после частичного шифрования/расшифрования являются наиболее (или иногда, наименее) часто угадываемыми с помощью дифференциалов, принимаются как правильные. Новый метод, описанный Бихамом и др., наоборот, выполняет поиск дифференциалов, которые дают никогда не случающиеся значения, а именно, значения, вероятность которых равна нулю. В варианте атаки с восстановлением ключа, если значение кандидата подключа приводит к выводу, что текстовая пара удовлетворяет такому дифференциалу, то подключ конечно будет неправильным. Эта процедура, называемая отсевом (sieving), находит правильный подключ путем исключения всех других подключей, которые удовлетворяют дифференциалу. Заметим, что это означает, что отношение S/N (сигнал/помехи) (Определение 4.7) такой счетной схемы равно S/N= 0, так как правильный подключ никогда не будет угадан; угадываются только неправильные подключи. Такие дифференциалы с вероятностью нуль называются невыполнимыми дифференциалами, а связанный с ними метод – криптоанализом на основе Невыполнимых Дифференциалов (ID). В [116] Кнудсен независимо описал такой же метод, примененный для шифра DEAL, r-циклового (r 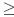6) шифра Файстеля, который использует DES как цикловую функцию.

Один из методов построения невыполнимых дифференциалов называется «встречей посредине». Он состоит в комбинировании двух дифференциалов, каждый выполняемый с вероятностью 1, которая не может одновременно достигаться. Поэтому их комбинация приводит к противоречию. Как только такая комбинация обнаруживается, она может использоваться как распознаватель для отбрасывания неправильных подключей и нахождения правильных подключей методом исключения. Другой подход, также предложенный Бихамом и др. в [18] базируется на полной структуре шифра. Процедура нахождения невыполнимых дифференциалов состоит в шифровании многих пар открытого текста, на всех возможных ключах, и отбрасывании всех получаемых разностей, потому что они не достижимы. Таким образом, путем исключения (опять отсева) остаются только дифференциалы, которые никогда не появляются. Тем не менее, такой поиск обычных невыполнимых дифференциалов требует перебора слишком многих дифференциалов и ключей. Бихам и др. предложили использовать усеченные дифференциалы, в которых разности определяются пословно³ и важным является только нулевое и ненулевое состояние разности. Как следствие число текстовых разностей сокращается до числа комбинаций нулевых/ненулевых словарных разностей. Тем не менее, это может не обеспечить противодействие дифференциалам, в которых входная пара приводит к выходным данным, имеющим нулевую разность в пределах границ слова. Для решения обеих проблем было предложено проанализировать уменьшенные варианты шифра, в которых сохраняется характер компонентов шифра и его полная структура, но размер уменьшается для возможности осуществления исчерпывающего поиска невыполнимых дифференциалов.

Сохранение характера компонентов шифра означает, например, что (большие) перестановки заменяются (малыми) перестановками, (большие) функции заменяются (меньшими) функциями, сохраняется также сходство линейных преобразований и других операций. Этот метод называется стягиванием.

Атаки на основе невыполнимых дифференциалов были применены к нескольким шифрам, как со структурой Файстеля, так и SPN структурой, таким как Skipjack [18], IDEA и Khufu [19], Twofish [21], Misty [130], Rijndael [22] и Crypton [207].

Бумеранг Атака

В [223] Вагнер представил новый метод анализа блочных шифров, называемый Бумеранг атакой. Это атака с выбранным текстом, которая является развитием метода дифференциального криптоанализа. В традиционной дифференциальной атаке пары открытых текстов выбираются с фиксированной разностью, и анализируется распространение дифференциальных комбинаций через шифр. Цель атаки – предсказать получаемую с помощью алгоритма выработки отобранных ключей разность шифртекстов с непренебрежимой вероятностью. Если эта цель может быть достигнута, то шифр можно отличить от случайной перестановки, и во многих случаях атака восстановления ключа может быть осуществлена в шифр. В отличие от этого, Бумеранг-атака не требует покрытия полного шифра с помощью одного дифференциала. Вместо этого атака использует дифференциалы высокой вероятности, которые не обязательно взаимосвязаны друг с другом, но которые вместе могут покрыть полный шифр (или большинство шифров). При этом она предполагает использование расширенных структур, чем в стандартной дифференциальной атаке. Точнее, бумеранг-атака является дифференциальной атакой, в которой пытаются сгенерировать квартетную структуру промежуточного значения полу-пути через шифр. Квартетная структура иллюстрируется на Рис. 1. Кроме того, Бумеранг-атака требует способности осуществления запросов выбранных открытых текстов и выбранных шифртекстов.

Различают «нисходящую» и «восходящую» Бумеранг атаки. В «нисхо-дящей» Бумеранг атаке запросы выбранных шифртекстов являются адаптивными в том смысле, что сначала получаются шифртексты, представляющие собой результаты запросов выбранных открытых текстов от оракула шифрования. После чего выполняются соответствующие модификации этих шифртекстов и затем представление их оракулу расшифрования. «Восходящая» Бумеранг атака начи-нается с запросов выбранных шифртекстов, и затем выполняются адаптивные запросы выбранных открытых текстов. Не нарушая общности, далее будет дано описание «нисходящей» Бумеранг-атаки, процедура для «восходящих» Бумеранг-атак аналогична.

Пусть E_K будет алгоритмом шифрования, который можно разбить на две части, 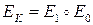,где каждая част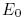и и 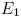не обязательно соответствуют половине шифра. Ясно, что .Кроме того, допустим, что разностным оператором является исключающее ИЛИ. Основная задача (см. Рис. 1) состоит в том, чтобы покрыть пару открытых текстов 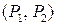(в других обозначениях (P, P¢)) дифференциальной характеристикой для алгоритма шифрования 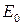, а пары открытых текстов 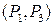и 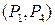((P, Q) и (P¢, Q¢)) - дифференциальной характеристикой для алгоритма шифрования 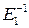. В этом случае можно показать, что пара открытых текстов 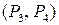((Q, Q¢)) полностью устанавливается использованием дифференциальной характеристики 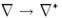для 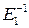. Мы можем подытожить этот сценарий как следующий:

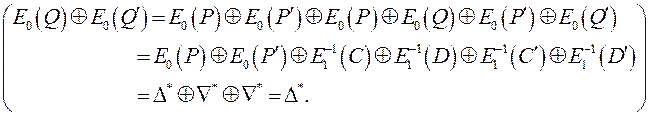
Таким образом, получается то же различие в открытых текстах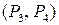
((Q, Q¢)) какое обнаруживается в исходных открытых текстах 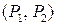((P, P¢)), что и определяет, почему атака названа бумеранг-атакой.

Атака начинается с выбора пары открытого текста 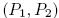такой, что 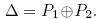Допустим, что существует дифференциальная комбинация (комбинация разностей) 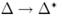, которая распространяется через часть 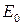алгоритма шифрования с не пренебрежимой вероятностью p, и, следовательно, 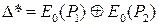. Пусть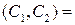 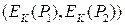. Далее выбирается пара шифртекстов 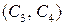, имеющихразности 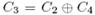такие, что комбинация 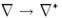распространяетсячерез 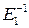с не пренебрежимой вероятно-стью q и, таким образом,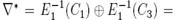 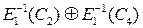. Соответствую-щая пара открытых текстов 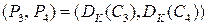запрашивается оракулом расшифрования. Если все три предыдущие разностные комбинации возникают, как задумано, то разности между частями шифра 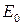и 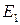как раз имеют структуру, представленную (Рис.1 (a)). Здесь можно сослаться на Вагнера [223]: «...вот почему мы называем это атакой Бумеранга: когда вы пошлете его правильно, он всегда возвратится назад».

Последняя дифференциальная комбинация 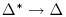вычисляется путем расшифрования E₀ для данных в паре, и Бумеранг атака обнаруживается путем верификации условия 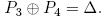Правая четверка определяется как четырехэлементный кортеж 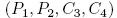, для которого все четыре дифференциальные комбинации выполняются одновременно. Четверка для «нисходящей» Бумеранг-атаки означает два выбранных открытых текста 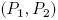и два адаптивно выбранных шифротекста, 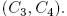Вероятность обнаружения разности в паре открытого текста 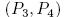может оцениваться как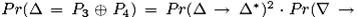 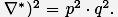Заметим, что разност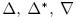и и 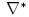являются некоррелированными и могут выбираться для максимизации вероятности успеха атаки произвольно. В Бумеранг-атаке допускалось следующее свойство: 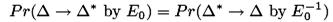которое справедливо для обычных дифференциальных характеристик, но не обязательно выполняется для усеченных дифференциалов.

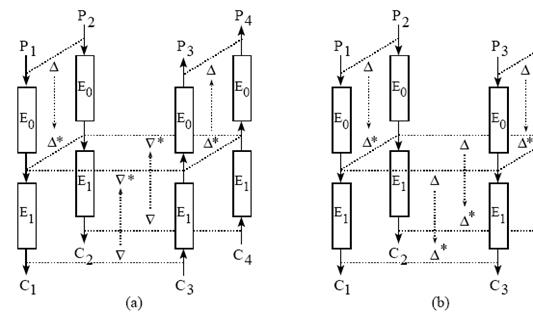
Рис. 1: (a) Нисходящий Бумеранг и (b) Усиленный Бумеранг

Сегодня существует ряд поправок (уточнений) к базовому методу Бумеранга

В [108] Келси и др. представили вариант метода Бумеранга, называемый усиленной Бумеранг-атакой. Хотя основная Бумеранг-атака использует два дифференциала первого порядка, которые считаются несвязанными (не могут быть сцеплены), тем не менее, они взаимосвязаны дифференциальным отношением второго порядка, включающим тексты между E и E , посредством запросов адаптивно выбранных шифротекстов. Идея усиленных Бумеранг атак заключается в использовании большего количества пар выбранных открытых текстов для случайного получения дифференциального отношения второго порядка между двумя дифференциалами.

Эта атака использует структуры[1]⁾ текстов [24] и структуры текстовых конструкций для получения дифференциальных отношений второго порядка для многих текстовых пар сразу (Рис. 4.17(b)). В отличие от основного метода Бумеранга усиленные Бумеранг-атаки используют только запросы с выбранным открытым текстом (или только с выбранным шифротекстом), но не сразу оба. Кроме этого свойства основной метод требует намного меньше запросов, чем усиленные Бумеранг-атаки, потому что в последнем случае должно запрашиваться достаточно много подходящих пар с целью достижения высокого значения вероятности получения внутренней коллизии, и значит, нужного дифференциального отношения высокого порядка между двумя дифферен-циальными комбинациями. Вероятность получения правильной четверки равна 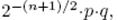где n – размер блока.

В [20] Бихам и др. описали прямоугольную атаку, которая, аналогично усиленной Бумеранг-атаке, использует запросы только выбранных открытых текстов (или выбранных шифротекстов), но не оба сразу. 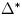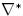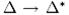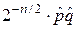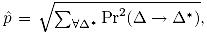В прямоугольной атаке учитываются все возможные промежуточные разности и , так чтобы и Такой подход лучше, чем усиленный метод Бумеранга, и вероятность получения правильной четверки в прямоугольной атаке равна , где и

[1]⁾ структура является средством, чтобы уменьшать общее число выбранных текстовых блоков. Структура состоит из набора блоков, которые обеспечивают несколько пар для одного или более заданных различий (разностей). Например, структура которая состоит из четырех 4-словных блоков, в которых первое слово содержит произвольные не равные нулю величины, а другие слова являются нулями, может сгенерировать до шести пар с различием ( 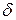; 0; 0; 0), в то время как стандартный метод должен потребовать 12 текстовых блоков.