Приклади нелiнiйних коливань

В багатьох механiчних системах рух описується нелiнiйними диференцiальними рiвняннями. Поява в рiвняннях нелiнiйних членiв зумовлена наявнiстю сили пружностi або сили опору, що змiнюються за нелiнiйним законом.

Нелiнiйнi диференцiальнi рiвняння розв’язують наближено. В цьому випадку кажуть, що проводять лiнеаризацiю нелiнiйних диференцiальних рiвнянь. Замiна точних нелiнiйних диференцiальних рiвнянь наближеними диференцiальними рiвняннями впливає не тiльки на кiлькiснi результати, але й спотворює якiсну сторону розглядуваних явищ. Наприклад, у випадку лiнiйних коливань частота коливань не залежить вiд початкових умов. У випадку ж нелiнiйних коливань частота залежить вiд початкових умов.

До цього часу відсутні загальнi методи iнтегрування нелiнiйних диференцiальних рiвнянь. Але за останнi роки були розробленi наближенi i графiчнi методи.

В першому наближеннi вважають, що модуль сили пружностi змiнюється за законом Гука, тобто за лiнiйним законом в залежностi вiд змiщення Δx (штрихована пряма на рис. 6.1).

Це приводить задачу до лiнiйного диференцiального рiвняння вiльних коливань:

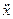+k²x = 0.

Разом з тим бiльш точно закон Гука записується так:

F_x =- c₁x- c₃x³ -c₅x⁵, (6.1)

тобто, тут сила зростає швидше, нiж за лiнiйним законом; ця характеристика сили називається ”жорсткою”. Така характеристика спостерiгається у гуми (крива 1-1 рис. 6.1).

Iнакше закон Гука записується так:

F_x =- c₁x + c₃x³ + c₅x⁵, (6.2)

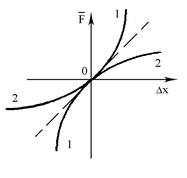тобто, тут сила зростає повiльнiше, нiж за лiнiйним законом; ця характеристика називається ”м’якою”. Вона спостерiгається, наприклад, в чавунi (крива 2-2 рис. 6. 1).

У випадку ”жорсткої” характеристики пружної сили

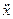+k²x+gx³+px⁵+... = 0,

(g = с₁/m>0), (6.3)

Рис. 6. 1.

а у випадку ”м’якої” характеристики сили пружностi

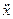+k²x- gx³ - px⁵ -... = 0,

(g = с₁/m>0), (6.4)

тобто в загальному випадку

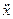+f(x) = 0, (6.5)

де f(х) - деяка нелiнiйна функцiя х.

Прикладом нелiнiйних коливань є також маятник, диференцiальне рiвняння коливань якого має вигляд

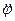+k²sinφ = 0.

Розглядаємо

sinφ = φ-(φ³/1·2·3)+(φ⁵/5!)+…;

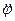+k²φ-(k²/6)φ³+(k²/120)φ⁵= 0.

В деяких випадках характеристика сили пружностi є лiнiйною на окремих дiлянках. Прикладом може бути тягар А мiж двома пружинами, який не прикрiплений до їх кiнцiв. В цьому випадку характеристика сили пружностi складається з двох прямолiнiйних вiдрiзкiв (рис. 6.2).

Розглянемо приклади нелiнiйних коливань систем з одним ступенем вiльностi.

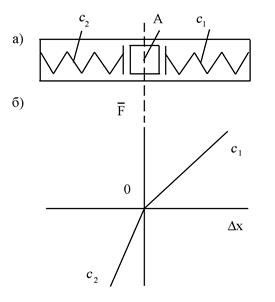
Рис. 6. 2.