Приклади структурного аналізу плоских механізмів
Існує певний порядок проведення структурного аналізумеханізмів.
1. Визначають число ступенів вільності механізму (або кінематичного ланцюга).
2. Виділяють початкові ланки, кількість яких визначається числом ступенів вільності механізму (кінематичного ланцюга). Нагадаємо, що початкова ланка і стояк утворюють механізм І класу.
3. Розбивають механізм на структурні групи. Відокремлення структурної групи частіше всього розпочинають з ланок і пар, найвіддаленіших від початкової ланки. Розпочинають із спроби від'єднати від механізму групи II класу. Від'єднуючи структурні групи, треба перевірити число ступенів вільності W тої частини механізму, яка залишилась, при цьому W не повинно змінюватися. Групи відділяють до того часу, поки не залишиться одна початкова ланка і стояк (механізм І класу), якщо W = 1, чи кілька початкових ланок, кількість яких дорівнює одержаному числу ступенів вільності. Якщо спроби від'єднання груп II класу не дадуть такого результату, то треба переходити до спроб від'єднання груп III класу, потім IV тощо.
4. Визначають клас і порядок структурних груп і клас механізму.
5. Записують формулу будови механізму.
Приклад 2.1. Виконати структурний аналіз механізму поперечно-стругального верстату (рис. 2.36, а), якщо початкова ланка-кривошип ОА.
Розв'язання. Механізм поперечно-стругального верстата складаються з п'яти рухомих ланок (п = 5) і семи кінематичних пар V класу (р5 = 7): O(0, 1), А(1, 2), А3(2, 3), B(0, 3), С(3, 4), D(4, 5), D0(0, 5). Число ступенів вільності такого механізму визначаємо за формулою Чебишева
W = 3п - 2р5 - р4 =3 * 5 - 2 * 7 = 0 = 1.
У такому механізмі має бути одна початкова ланка .Розкладаємо механізм на групи Ассура. Спочатку відокремлюємо ланцюг, який складається з двох ланок 4, 5 і трьох кінематичних пар С, D, D0 (рис. 2.33, б); знаходимо число ступенів вільності для залишкової частини механізму:
W=3 * 3 – 2 * 4 = 1.
Враховуючи, що W не змінилось, виділений ланцюг, який складається з ланок 4, 5, є групою II класу II порядку.
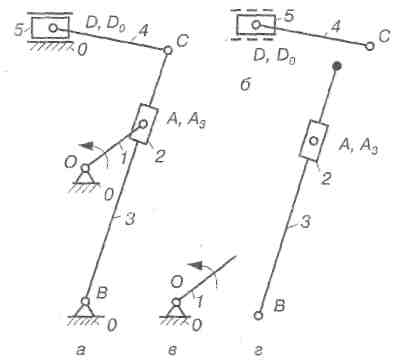
Рис.2.36. Структурний аналіз механізму поперечно-стругального верстата:
а) кінематична схема механізму; б, г) структурні групи; в) механізм І класу
Далі відокремлюємо ланцюг, який складається з ланок 2, З і трьох пар А, Аз, В (рис. 2. 36, г). Після цього залишається одна початкова ланка (рис. 2.36, в), в якої W= 1, а тому ланцюг 2-3 є також групою II класу.
Отже, механізм поперечно-стругального верстата складається з механізму І класу і двох груп II класу II порядку, тому його слід віднести до механізмів II класу.
Для такого механізму можна записати таку формулу будови:
І(1) -> II(2,3) -> П(4,5),
де цифрою І позначено механізм 1 класу, цифрою II - клас групи. Номера ланок, що входять до складу механізму І класу та груп, взято у дужки.
Приклад 2.2. Виконати структурний аналіз механізму двигуна (рис. 2. 37,а), якщо початковою ланкою є кривошип ОА.
Розв'язання. Механізм складається із семи рухомих ланок (п= 7) і десяти пар V класу (р5=10): О(0, 1), А(1, 2), В(2, 3), В0(3, 0), С(2, 4), D(4, 5), Е(5, 0), F(5, 6), G(6, 7), G0(1, 0). Знаходимо ступінь вільності механізму за формулою Чебишева:
W=3п - 2р5 - р4 =3 * 7 – 2 * 10 - 0 = 1.
У цьому механізмі також повинна бути одна початкова ланка
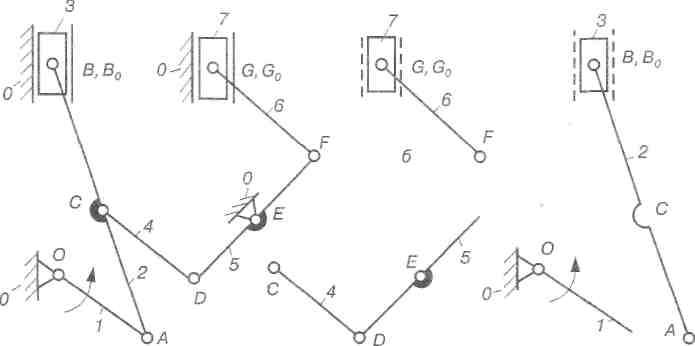
Розкладаємо механізми на групи Ассура Якщо початковою ланкою є кривошип 1, який із стояком 0 утворює механізм І класу (рис. 2.37, г), то решта ланок утворюють три структурні групи її класу II порядку (рис. 2.37, б, в, д). Такий механізм слід віднести до механізму II класу. Його формула будови має такий вигляд
І(1)-»ІІ(2,3) ->II4,5) -»III(6,7).
|
Якщо вибрати початковою ланкою, наприклад, ланку 7, то механізм треба віднести до Ш класу, тому що в цьому випадку ланки і пари, до складу яких вони входять, утворюють дві групи, одна з цих група III класу (рис. 2.38, а), друга - II класу (рис. 2.38, б). Повзун 7 (рис. 2.38, в) разом із стояком 0 утворює механізм 1 класу. Формула будови такого механізму
а в г д
Рис.2.37. Структурний аналіз механізмудвигуна (початкова ланка - кривошип 1):
а) кінематична схема механізму; б, в, д) структурні групи; г) механізм І класу
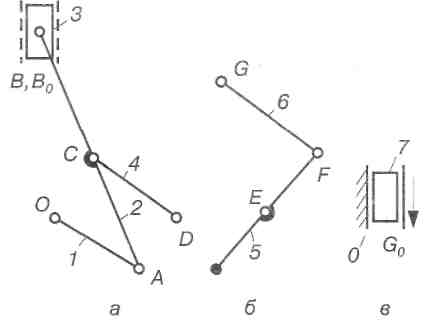
Рис.2.38. Структурний аналіз механізму двигуна (початкова ланка - повзун 7):
а; б) структурні групи; в) механізм 1 класу
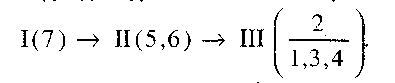
При початковій ланці 5 механізм також буде III класу, формулу будови якого можна записати так (див. рис. 2.37, а):
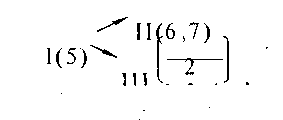
Приклад 2.3, Виконати структурний аналіз кулачково-важільного механізму, схему якого зображено на рис. 2.39, а. Початковою ланкою вибрати кулачок 1.
Розв'язання. Механізм складається з п'яти рухомих ланок (п= 5), шести кінематичних пар V класу (р5 = 6) - О(0, 1), B(2,3 ), С(3, 4), D(4, 0), Е (3, 5), F (5, 0) - і одної пари. IV класу (р4 = 1) - К (1, 2). Якщо підрахувати число ступенів вільності за цими даними, одержимо
W=3п-2р5-р4 =3*5-2*6-1 = 2.
Тут ролик 2 створює зайвий ступінь вільності (ролик може ковзати відносно кулачка і перекочуватись по ньому).
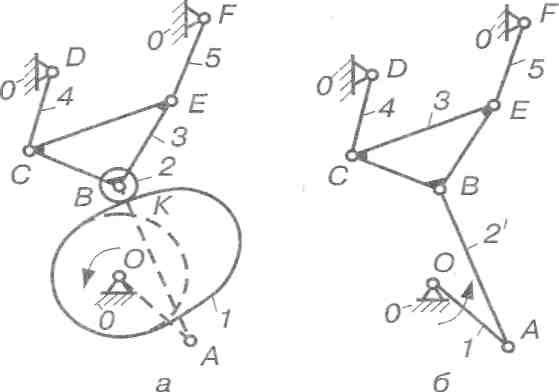
Рис. 2.39. Структурний аналіз кулачково-важільного механізму:
а) основний механізм; б) замінний
Будуємо замінний механізм. Для цього вищу пару К (пару IV класу) замінюємо нижчими парами V класу. Центр кривизни ролика 2 знаходиться в точці В, центр кривизни профілю кулачка 1 - у точці А. У точках А і В розміщаємо центри шарнірів додаткової умовної ланки 2' (рис. 2.39, б), які з'єднуємо з кулачком 1 (ланка ОА) і ланкою 3.
У замінному механізмі маємо п = 5,p5, p4 = 0, тоді
W=3п-2р5-р4 = 3*5-2*7-0 = 1.
Отже, у такому механізмі потрібна лише одна початкова ланка Залишимо такою ланкою кулачок 1 (на рис. 2.39,6 - кривошип ОА), який разом зі стояком О утворює механізм 1 класу.
Кінематичний ланцюг, що залишається після від'єднання механізму І класу, не можна розкласти на групи II класу. Ланки 2', 3, 4, 5 утворюють групу III класу III порядку, причому ланка З є базисною, тому механізм, схему якого зображено на рис. 2.39,а, треба віднести до III класу. Формула будови такого механізму
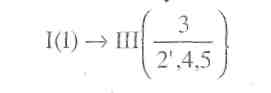
Питання для самоперевірки
І. Ступені вільності та умова зв'язку. Наведіть приклади кінематичних пар, які мають різні ступені вільності. 2. За якими ознаками класифікують кінематичні пари? 3. Як визначається клас кінематичної пари (за класифікацією 1.1. Артоболевського)? 4. Які кінематичні пари відносять до нижчих, а які до вищих? Які позитивні якості та недоліки цих пар? 5. Чим відрізняється силове замикання ланок від геометричного?Їїх переваги та недоліки. 6. Класифікація кінематичних ланцюгів. В яких механізмах використовують незамкнуті кінематичні ланцюги? 7. Запишіть структурні формули для плоских і просторових механізмів (формули Чебишева і Сомова-Малишева). 8. Яке практичне значення має ступінь вільності кінематичного ланцюга? 9. Яким чином одержати з кінематичного ланцюга механізм? 10. Чи можна в механізмі з одним ступенем вільності змінити положення ланок, не змінюючи положення вхідної ланки? 11. Поняття про зайві ступені вільності та пасивні умови зв'язку. 12. Чому еквівалентна вища пара при її заміні нижчими? 13. Основний принцип утворення механізмів за Л. Ассуром. 14. Поняття про структурну групу та механізм 1 класу. 15. Як визначається клас і порядок структурної група, клас механізму (за Ассуром-Артоболевським)7 16. Для чого потрібні знання про структуру механізмів?
Розділ 3
Дата добавления: 2016-06-15; просмотров: 4716;











