Приклади гідрологічних розрахунків
Вправа 2.1. За матеріалами багаторічних спостережень визначити характеристику стоку р. Ірпінь біля с. Мостище (Київська область). Площа р. Ірпінь біля с. Мостище F= 2840 км2, норма опадів у басейні за 1964– 1988 роки χ =590 мм. Середньорічні витрати води р. Ірпінь для даного гідрологічного посту наведені у табл.. 14.1
Таблиця 14.1
| № п/п | Роки | Середньорічні витрати Q, м3/с | № п/п | Роки | Середньорічні витрати Q, м3/с |
| 2,64 | 8,76 | ||||
| 5,22 | 8,26 | ||||
| 8,69 | 10,3 | ||||
| 7,33 | 15,59 | ||||
| 7,27 | 12,09 | ||||
| 10,19 | 9,74 | ||||
| 9,51 | 6,37 | ||||
| 11,5 | 13,5 | ||||
| 5,85 | 9,19 | ||||
| 5,85 | 7,21 | ||||
| 3,41 | 7,97 | ||||
| 4,17 | 8,74 | ||||
| 4,04 | |||||
| ∑ =203,12 |
Розв’язання
1. Середньо багаторічна витрата води
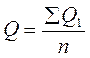
Де ∑ Q1 – сума середньорічної витрати води, м3/с;
п – кількість спостережень.
Отже
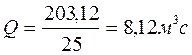
2. Сумарний об’єм води за рік
W=Q*t
Де t– кількість секунд в році
Отже W= 8,12*31,536*106 = 256,07*106 м3
3. Середній багаторічний модуль стоку
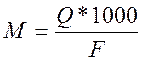
Де F – площа водозбору , км 2
Отже 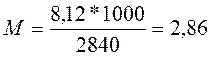 л/(с*км2)
л/(с*км2)
4. Середній багаторічний шар стоку
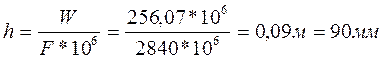
5. Середній багаторічний коефіцієнт стоку
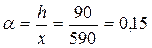
6. Модульний коефіцієнт
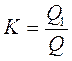
Де Q1 – середня річна витрата води, м3/с.
Наприклад, за 1965 рік витрата Q =5,22 м3/с. Отже модульний коефіцієнт цього року:
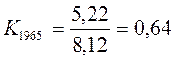
За 1981 р. модульний коефіцієнт
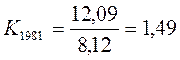
Аналогічно визначені модульні коефіцієнти за все роки спостережень і наведені в таблиці 14.2
| Модульні коефіцієнти | Середньорічні витрати, м3/с | Роки | Модульні коефіцієнти | Середньорічні витрати, м3/с | Роки |
| 0,32 | 2,64 | 1,08 | 8,76 | ||
| 0,64 | 5,22 | 1,02 | 8,26 | ||
| 1,07 | 8,69 | 1,27 | 10,3 | ||
| 0,90 | 7,33 | 1,92 | 15,59 | ||
| 0,89 | 7,27 | 1,49 | 12,09 | ||
| 1,25 | 10,19 | 1,20 | 9,74 | ||
| 1,17 | 9,51 | 0,78 | 6,37 | ||
| 1,42 | 11,5 | 1,66 | 13,5 | ||
| 0,72 | 5,85 | 1,13 | 9,19 | ||
| 0,72 | 5,85 | 0,89 | 7,21 | ||
| 0,42 | 3,41 | 0,98 | 7,97 | ||
| 0,51 | 4,17 | 1,08 | 8,74 | ||
| 0,50 | 4,04 | 1,27 |
Вправа 2.2. За картою ізоліній середнього багаторічного стоку визначити характеристики стоку річки, план басейну якої показано на рисунку 14.1 (масштаб 1:500000).
Річка знаходиться на Волино-Подільській височині.
Розв’язання. Середньо багаторічний модуль стоку визначаємо за формулою

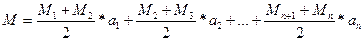
а1+а2+…+аn
Де М1, М2…Мn – модулі стоку на границі ділянок, що відсікаються ізолініями модулів стоку, л/(с*км2);
а1+а2+…+аn – площі ділянок басейну між ізолініями і водоміром, км 2 .
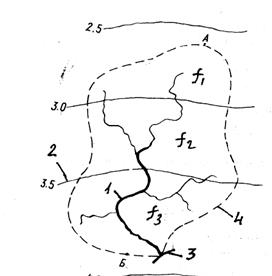
Рисунок 13.1. Карта ізоліній середнього багаторічного стоку річки, М 1:500000
Басейн двічі перетинається ізолініями модулів стоку і знаходиться між ізолініями 2,5 л/(с*км2).
У верхній частині вододіл найближче підходить до ізолінії 2,5 л/(с*км2) точкою А. Значення М для цієї точки визначаємо між ізолініями 2,5 і 3 л/(с*км2). М1=2,62 л/(с*км2), , М2=3 л/(с*км2), і М3=3,5 л/(с*км2).
Модуль стоку нижньої частини басейну (точка Б) знаходимо інтерполяцією між ізолініями 4 і 3,25 л/(с*км2).
М4=3,9 л/(с*км2).
Площі f1, f2, f3 можна позначити розбивкою складних фігур на прості геометричні: трикутники, трапеції, прямокутники та ін. Треба лінійкою виміряти розміри цих фігур і, з врахуванням масштабу, визначити за формулами площі.
Крім того, їх можна визначити за допомогою міліметрового паперу (палетки). Для цього план басейну річки потрібно перенести на міліметровий папір і викреслити його як палетку (підрахувати кожну площу в см2). У даному випадку площі знайдено за допомогою палетки:
a1=6,5 см2 , a2= 11 см2, a3=12,5 см2
Потрібно врахувати масштаб:
а1 = 6,5*25=162,5 км2
а2 = 11*25=275 км2
а3 =12,5 *25=312,5 км2
Отже модуль стоку буде:
М= 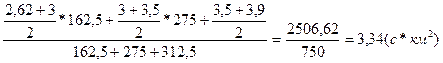
Згідно з таблиці 18 (Кузник И.А.) до норми стоку для басейнів Волино – Подільської височини з площею водозбору менше 2000 км2 потрібно вводити поправку.
М=Мγ
Де М – норма стоку
γ – поправочний коефіцієнт
Отже М=3,34*0,85=2,84 л (с*км2)
Середньобагаторічна витрата води ставить:
Q= 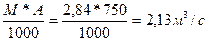
Середній багаторічний об’єм стоку:
W=Qt =2,13*31,536*106=67,17*106 м3
Середній багаторічний шар стоку:
Y= 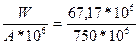 =0,089м=89 мм.
=0,089м=89 мм.
Вправа 2.3. Визначити характеристики стоку при недостатній кількості спостережень за стоком річки.
Методом гідравлічної аналогії визначити середні багаторічні характеристики стоку річки Здвиж біля с. Гавронщина. Середньорічні витрати води в р. Здвиж наведені в таблиці 13.3, площа водозбору 837 км2. За річку-аналог взяти р. Ірпінь, середньорічні витрати якої наведені в таблиці 13.1, середньо багаторічна витрата річки – аналога 8 ,12 м3/с.
Розв’язання
1. На аркуші міліметрового паперу (рис. 14.2) будуємо графік розв’язку між величинами витрат обох річок. По горизонтальній осі відкладаємо витрати річки, яку потрібно вивчити, по вертикальній –річки Ірпінь за відповідний рік.
Наприклад, за 1972 рік по осі абсцис відкладено 1,77, а по осі ординат –5,85. На перетині перпендикулярів, проведених з цих точок зв’язку для 1972 року. Відклавши всі точки для спільних років спостережень, проводимо пряму лінію так, щоб вона займала середнє положення між точками.
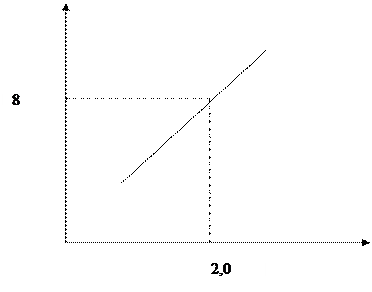






Рис. 14.2. Графік зв’язку між стоками р. Здвиж і р. Ірпінь
Щоб знайти багаторічну витрату річки Здвиж, на вертикальній осі відкладаємо величину, що відповідає середньо багаторічній витраті річки –аналога
Q=8,12 м3/с. З цієї точки проводимо горизонтальну пряму до перетину з прямою
зв’язку, а з точки перетину опускаємо перпендикуляр на горизонтальну вісь.
Основа цього перпендикуляру і визначає середньо багаторічну витрату води річки, яку визначають Qв =2,15 м3/с.
2. Середньобагаторічний модуль стоку:
Мв = 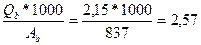 м3/с.
м3/с.
Таблиця 14.3
Середньорічні витрати води р. Здвиж в створі с. Гавронщина
| Роки спостережень | Середньорічні витрати, м3/с. | Роки спостережень | Середньорічні витрати, м3/с. |
| 2,41 | 1,04 | ||
| 1,77 | 1,22 | ||
| 1,50 | 2,48 | ||
| 1,15 | 1,88 |
3. Середній стік води за рік:
W в = Qв*t =2,15*31,536*106=67,8 *106
4. Середній багаторічний шар стоку:
Y= 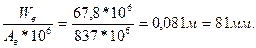
Вправа 2.4. Визначення розрахункових максимальних витрат води за даними спостережень.
1. За даними гідрометричних спостережень максимальних витрат талих вод розрахувати і побудувати аналітичну криву трьох параметричного гамма-розподілу.
2. За аналітичною кривою знайти максимальну витрату талих вод забезпеченістю 2%.
Для виконання вправи 4 «чотири» необхідно знайти дані спостережень як за 25 років.
Завдання:
Розрахувати максимальну витрату весняної повені забезпеченістю 1% і 2% за даними гідрометричних спостережень, які наведені в таблиці 14.4 гр.2 і3.
Розв’язання. Для визначення максимальної витрати води потрібно розрахувати аналітичну криву трьох параметричного гамма-розподілу та її ординати спів ставити з емпіричною кривою. Розрахунки параметрів аналітичної кривої і ординат емпіричної кривої виконувати за табл.14.4
1. Знаходимо середню багаторічну максимальну витрату води:
Qмакс = 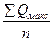 , м3/с
, м3/с
де∑Qмакc – сума максимальних витрат води в м3/с за n років
Отже Qмак = 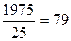 м3/с
м3/с
Таблиця 14.4
| №п/п | Рік | Максимальна витрата, Qмак м3/с | К1= 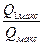
| Lg K1 | K1 Lg K1 | K1 в убуваючому порядку | Відповідний K1 рік | Емпірична забезпеченість |
| 0,52 | -0,284 | -0,184 | 1,57 | 3,85 | ||||
| 0,43 | -0,366 | -0,157 | 1,53 | 7,7 | ||||
| 0,96 | -0,018 | -0,017 | 1,47 | 11,54 | ||||
| 1,57 | 0,196 | 0,308 | 1,43 | 15,38 | ||||
| 1,05 | 0,021 | 0,022 | 1,34 | 19,23 | ||||
| 1,16 | 0,064 | 0,074 | 1,32 | 23,08 | ||||
| 1,47 | 0,167 | 0,245 | 1,20 | 26,92 | ||||
| 0,66 | -0,180 | -0,119 | 1,19 | 30,80 | ||||
| 0,77 | -0,113 | -0,087 | 1,16 | 34,61 | ||||
| 1,06 | 0,025 | 0,026 | 1,10 | 38,46 | ||||
| 0,53 | -0,275 | -.,146 | 1,06 | 42,31 | ||||
| 0,95 | -0,022 | -0,021 | 1,06 | 46,15 | ||||
| 1,34 | 0,127 | 0,170 | 1,05 | 50,00 | ||||
| 1,53 | 0,185 | 0,283 | 0,96 | 53,85 | ||||
| 1,19 | 0,075 | 0,089 | 0,95 | 57,69 | ||||
| 1,10 | 0,041 | 0,045 | 0,90 | 61,54 | ||||
| 0,72 | -0,143 | -0,103 | 0,79 | 65,38 | ||||
| 0,79 | -0,102 | -0,081 | 0,77 | 69,23 | ||||
| 1,32 | 0,121 | 0,160 | 0,72 | 73,08 | ||||
| 1,43 | 0,155 | 0,222 | 0,69 | 76,92 | ||||
| 0,60 | -0,222 | -0,133 | 0,66 | 80,77 | ||||
| 0,69 | -0,161 | -0,111 | 0,60 | 84,61 | ||||
| 0,90 | -0,046 | -0.041 | 0,53 | 88,46 | ||||
| 1,06 | 0,025 | 0,026 | 0,52 | 92,31 | ||||
| 1,30 | 0,079 | 0,095 | 0,43 | 96,15 | ||||
| -0,651 | 0,636 |
2. Модульні коефіцієнти кожного року спостережень знаходимо за формулою:
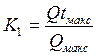
Наприклад, модульний коефіцієнт 1964 року буде:
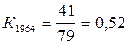
Значення модульних коефіцієнтів записуємо в гр.4 табл.14.4
Якщо значення К1 обчислені правильно, то сума буде дорівнювати кількості спостережень.
3. Знаходимо lg Ki і Ki lg Ki (гр.. 5 і 6 ) і підраховуємо їх суму:
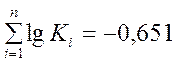
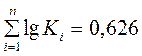
4. Модульні коефіцієнти розміщуємо в убиваючому порядку(гр.7) в гр.8 записуємо відповідний рік К1.
5 . Емпіричну забезпеченість (гр.9) розраховуємо за формулою:
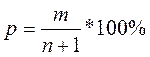
Де m – порядковий номер модульного коефіцієнта в убуваючому ряду;
n – кількість спостережень.
Наприклад, забезпеченість модульного коефіцієнта 1,57 (1977 р.) буде:
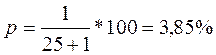
Модульний коефіцієнт 1,32 (1982 р.) буде:
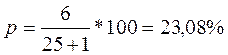
6. Визначаємо статистики
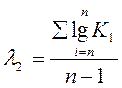
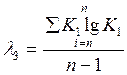
Отже
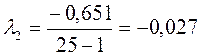
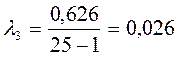
7. За номограмою 5 ( Е.Е. Овчаров, Н.Н. Захаровськая «Гідрологія і гідрометрія») залежно від λ 2 λ3 знаходимо Сv і Сs/Cv
Сv = 0,35; Сs = 2; Cv = 0,35*2 = 0,7
8. За додатком 3 ( Е.Е. Овчаров, Н.Н. Захаровськая «Гідрологія і гідрометрія»), залежно від при С=2С знаходимо ординати кривої забезпеченості трьох параметричного гамма-розподілу різної забезпеченості. Результат заносимо в таблицю 13.5
Таблиця 14.5
Ординати аналітичної кривої трьох параметричного гамма-розподілу
| Забезпеченість P 1% | Кр % | Забезпеченість P 1% | Кр % |
| 1,99 | 0,88 | ||
| 1,64 | 0,79 | ||
| 1,47 | 0,74 | ||
| 1,27 | 0,70 | ||
| 1,21 | 0,58 | ||
| 1,14 | 0,50 | ||
| 1,05 | 0,45 | ||
| 0,96 | 0,37 |
9 . За даними таблиці 12 будуємо аналітичну криву забезпеченості (рис 14.3)
| ||||||||||
| К | ||||||||||
| 1,5 | ||||||||||
| 0,5 | ||||||||||
| р,% |
Рисунок 14.3. Крива забезпеченості модульних коефіцієнтів максимальних витрат води
На графік аналітичної кривої наносимо точки емпіричної забезпеченості, координати яких є в таблиці 11, гр..7 і 9 на рис. 14.3 точки емпіричної кривої майже сов падають з аналітичною кривою. Це свідчить про те, що аналітична крива розрахована правильного.
10. За аналітичною кривою знаходимо модульні коефіцієнти розрахункової забезпеченості 1% і 2%
К1% =1,99; К2% = 1,91
11. Визначаємо розрахункові максимальні витрати весняної повені за формулою Qмакс p% = Qмакс *K p% ; м3/c ,
Де Qмакс – середньо багаторічна максимальна витрата, яка знайдена у першому пункті і дорівнює 79 м3/c;
K p% – модульний коефіцієнт розрахункової забезпеченості (визначені за аналітичною кривою).
Q1% =79*1,99=157,21 м3/c;
Q2% =79*1,91=150,89 м3/c.
Вправа 2.5. Визначення розрахункових максимальних витрат води при відсутності даних гідрометричних спостережень.
Для виконання вправи 5 потрібно мати величини: площу водозбору, похил водозбору і водного потоку, ґрунти басейну дані про озерність, лісистість і заболоченість басейну, координати розрахункового створу.
У вправі необхідно:
1. Розрахувати максимальну витрату талих вод забезпеченістю 1% при відсутності гідрометричних спостережень.
2. Розрахувати максимальну витрату дощових вод забезпеченістю 1% при відсутності гідрометричних спостережень.
Завдання 1.Визначити розрахункову максимальну витрату талих вод забезпеченістю 1% при відсутності гідрометричних спостережень, р. Уж біля с. Великий Черевач. Площа басейна А = 7980 км2, лісистість рівномірна Ал =26%, грунти супіспані, заболоченість Аб =16% (болота різних типів), координати центра басейна φ 50057’ півн.ш., λ= 29012’ сх. д. , озерність < 1%.
Розв’язання
Максимальну витрату талих вод обчислюємо за формулою:
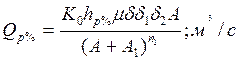
Де К0 – коефіцієнт дружності сніготанення, який знаходимо за таблицею 34 (Кузник И.А. и др.). Для рівнинних річок лісостепової зони К0 =0,012;
h p%– розрахунковий шар весняного стоку, мм.
h p%= h 0*K,% , мм,
де – середньо багаторічний шар весняного стоку, мм – модульний коефіцієнт розрахункової забезпеченості, знаходиться з додатка 3 ( Е.Е. Овчаров, Н.Н. Захаровськая «Гідрологія і гідрометрія») залежно від коефіцієнта Сv. Значення h0 іCv знаходимо за рисунком 55 (Кузник И.А. і др..)
h0=50 мм, Cv=0,55, K1% =2,7.
Тоді величина весняного стоку 1% забезпеченості буде:
h1% =K1% h0 = 2,7*50=135 мм;
μ– коефіцієнт що враховує нерівномірність статистичних параметрів шару стоку і максимальних витрат води, визначаємо за табл.. 3.11 ( Е.Е. Овчарова, Н.Н. Захаровськая «Гідрологія і гідрометрія»). Для лісостепової зони і забезпеченості 1% = 1,0; δ– коефіцієнт, що враховує вплив озер, ставків. Оскільки озерність менше 1% δ =1;
δ1 – коефіцієнт, що враховує лісистість басейну, визначається за формулою:
Значення а1 і n2 визначаємо за табл.. 3.13 Е.Е. (Овчаров, Н.Н. Захаровськая «Гідрологія і гідрометрія»), а1 =1, n2 =0,2.
А –лісистість басейну, %.
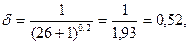
δ2 – коефіцієнт, що враховує заболоченість басейну, визначається за формулою:
δ 2 = 1- β lg(0,1Aб+1).
Для боліт різних типів β =0,7 (Овчаров, Н.Н. Захаровськая «Гідрологія і гідрометрія», табл.. 3.14).
Aб – заболоченість в %
δ 2 =1-0,7 lg(0,1*16+1) =1-0,7»*lg2,2=1-0,7»*0,41=0,61.
Значення показника ступеня редукції і додаткової площі водозбору А1, що враховує зниження редукції, знаходимо за додатком 7 (Е.Е.Овчаров, Н.Н. Захаровськая «Гідрологія і гідрометрія»), n1=0,25 A1=2 км2.
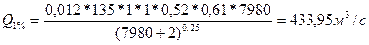
Завдання 2. . Визначити розрахункову максимальну витрату дощових вод забезпеченістю 2% при відсутності гідрометричних спостережень, р. Тур’я басейн Прип’яті ) в створі с. Бузаки. Площа басейна А=2630 км2, заболоченість Аб =26%, координати центра басейна φ 51013’ півн.ш., λ= 24051’ сх. д. , озерність < 1%.
Розв’язання. Оскільки площа водозбору перевищує 100 км2 і менша 2000 км2, то застосовуємо редукційну формулу
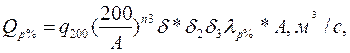
Де q2000 – модуль максимальної миттєвої витрати води 1%-ої забезпеченості при δ=δ2=δ3= 1 приведений до площі водозбору 200 км2, визначаємо інтерполяцію по карті за координатами створу рис.63 (И.А. Кузник и др.).
Q =0,23 л/(с*км2)
А – площа водозбору, км2;
n3 – коефіцієнт редукції модуля максимальної миттєвої витрати води, визначаємо за координатами створу, рис.14.4 , n3 =0,5;
δ – коефіцієнт, що враховує озерність басейну. Озерність менше 1%, тому δ =1;
δ2 – коефіцієнт, що враховує заболоченість басейну Визначаємо за формулою:
δ2 = 1-0,5lg(0,1 A б+1)
Отже
δ2 = 1-0,5lg(0,1 *26+1)= 1-0,5*0,41=0,8
δ3– коефіцієнт, який враховується тільки для гірських річок, Тур’я річки рівнинні δ3=1;
λр% перехідний коефіцієнт від максимальної миттєвої витрати розрахункової забезпеченості.
Щоб визначити потрібно спочатку по карти рис.14.5 за координатами створу знайти номер району, а потім за таблицею 13.6 залежно від номера і розрахункової забезпеченості, λр%
Річка знаходиться в 6 -ому районі λр% =0,7.
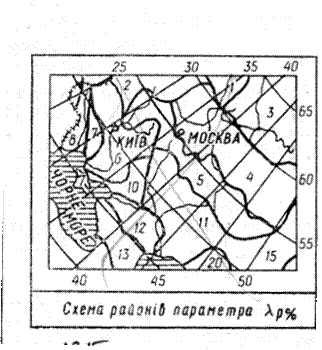
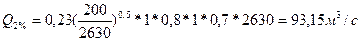
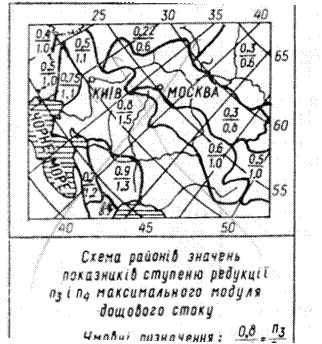
Рис. 14.4.Схема районів значень рис. 14.5. Схема районів параметра λр%
показників ступеню редукції макс-
имального модуля дощового стоку
Перехідний коефіцієнт максимальної витрати забезпеченості (Р=1% до до розрахункової
| Номер районі за рисунком 15.5 | Перехідний коефіцієнт λр% при забезпеченості, яка дорівнює | |||||
| 0,1 | ||||||
| 2,5 | 1,0 | 0,7 | 0,58 | 0,42 | 0,30 | |
| 2,41 | 1,0 | 0,74 | 0,63 | 0,50 | 0,32 | |
| 1,6 | 1,0 | 0,82 | 0,74 | 0,64 | 0,47 | |
| 1,45 | 1,0 | 0,85 | 0,79 | 0,70 | 0,55 | |
| 2,6 | 1,0 | 0,7 | 0,58 | 0,40 | 0,26 |
Дата добавления: 2016-07-27; просмотров: 2944;