Три форми диференцiальних рiвнянь

ДИНАМIКА МАТЕРIАЛЬНОЇ ТОЧКИ

Предмет динамiки. Маса

Динамiка - це роздiл теоретичної механiки, в якому вивчаються закони механiчного руху тiл пiд дiєю прикладених до них сил.

Основнi закони динамiки були сформульованi I. Ньютоном в безсмертнiй працi ”Математичнi начала натуральної філософії” (1687 р.).

Маса - фiзична характеристика матерiальних об’єктiв, яка є мiрою їх iнерцiйних i гравiтацiйних властивостей. Виразником iнерцiйних властивостей тiла маса виступає в законах динаміки; виразником гравiтацiйних властивостей маса входить в закон тяжiння.

За І. Ньютоном маса тiл вимiрюється порiвнянням їх ваги на терезах з коромислом.

У одного тiла маса гравiтацiйна та маса iнерцiйна збiгаються.

Тiло з масою m має енергiю Е = mс² ( тут с = 3·10⁸ м/с - швидкiсть свiтла в вакуумi).

Закони Ньютона

Перший закон Ньютона - закон інерції: будь-яке тiло продовжує зберiгати свiй стан спокою або рiвномiрного прямолiнiйного руху, поки i оскiльки його не спонукають змiнити цей стан прикладенi сили. Тут під термiном ”будь-яке тiло” треба розумiти матерiальну точку.

Перший закон стверджує динамiчну рiвноправнiсть стану спокою i рiвномiрного прямолiнiйного руху. Два стани - спокою i рiвномiрного прямолiнiйного руху - Ньютон розглядає як природнi стани всякого тiла. Здатнiсть тiл перебувати в цих природних станах i є те, що називається iнерцiєю тiл.

Закон iнерцiї справедливий тiльки вiдносно цiлком певної системи вiдлiку – ”iнерцiальної” системи. При розглядi бiльшостi технiчних задач iнерцiальною можна вважати систему, незмiнно пов’язану із Землею.

Другий закон - закон дiї сил: змiна кiлькостi руху матерiальної точки пропорцiональна прикладенiй рушiйнiй силi i вiдбувається в напрямi тiєї прямої, по якiй ця сила дiє

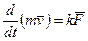, (2.1)

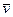
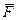
де m - маса матерiальної точки , - її швидкiсть, - сила, яку прикладено до точки, k - коефiцiєнт пропорцiональностi.

В усiх системах одиниць вибiр одиниць вимiрювання сили i маси узгоджено в такий спосiб, що коефiцiєнт пропорціональності k дорiвнює безрозмiрнiй одиницi.

При m = const i d 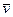/dt = 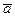( 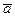- прискорення матерiальної точки) маємо

m 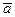= 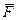. (2.2)

Рiвнiсть (2.2) читається так: у кожний момент часу добуток маси матерiальної точки та її прискорення дорiвнює рушiйнiй силi, а напрям вектора прискорення збiгається з напрямом сили.

Рiвнiсть (2.2), яка виражає другий закон Ньютона, справедлива лише за умови, що рух матерiальної точки вiднесено до iнерцiальної системи вiдлiку.

Третiй закон - закон взаємодiї тіл: дiї завжди вiдповiдає рiвна їй i протилежно направлена протидiя; iнакше кажучи, - сили взаємодiї двох матерiальних точок завжди мiж собою рiвнi i направленi в протилежнi сторони.

Третiй закон Ньютона стверджує, що в природi iснує тiльки взаємодiя тiл, причому дiя i протидiя за величиною рiвнi, а за напрямком протилежнi. Це справедливо і у випадку спокою, і у випадку руху тiл. Наприклад, Земля i камiнь, що падає на неї, є цiлком рiвноправними тiлами: сила притягання каменя до Землi дорiвнює силi притягання Землi до каменя. З цього i з рiвняння (2.2) випливає, що прискорення взаємодiючих тiл - Землi i каменя - обернено пропорцiональне їх масам.

Четвертий закон - закон незалежностi дiї сил: якщо на матерiальну точку дiють кiлька сил одночасно, то вони надають точцi такого складного руху, який складається кiнематично з рухiв, що їх кожна сила окремо здатна надати точцi без початкової швидкостi; якщо ж точка вже має швидкiсть i на неї дiє ще й сила, то рух точки складається кiнематично з руху за iнерцiєю i руху вiд дiї сили.

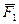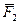Математичний змiст принципу незалежностi дiї сил такий: при одночаснiй дiї на матерiальну точку сил i прискорення точки дорiвнюватиме геометричнiй сумi тих прискорень, якi були б при роздiльнiй дiї сил:

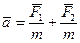. (2.3)

Вiдомо, що геометрична сума прикладених до точки сил називається рiвнодiйною:

= + .

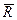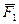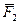Тоді

m = .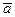

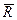Якщо на точку дiють одночасно декiлька сил, то другий закон Ньютона записують у виглядi:

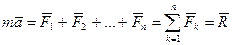. (2.4)

Питання для самоконтролю

1. Що є мірою інерційних і гравітаційних властивостей матеріальних об’єктів?

2. Запишіть формулу для визначення енергії тіла певної маси.

3. Сформулюйте основні закони механіки Ньютона.

4. Що стверджує перший закон Ньютона?

5. Що називається інерцією тіла?

6. В якому випадку закон інерції є справедливим?

7. Яку систему вважають інерціальною при розв’язанні більшості задач?

8. Сформулюйте закон дії сили.

9. Яке значення має коефіцієнт пропорціональності k в законі дії сили?

10. Як пов’язаний напрям вектора прискорення матеріальної точки з напрямом рушійної сили?

11. В яких умовах справедлива рівність, що виражає другий закон Ньютона?

12. Які положення стверджує третій закон Ньютона?

13. Запишіть, як математично виражається принцип незалежності дії сил.

14. Як записати другий закон Ньютона при одночасній дії на матеріальну точку кількох сил?

Три форми диференцiальних рiвнянь

Векторна форма

Запишемо другий закон Ньютона так:

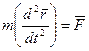, (3.1)

де m – маса точки, d² 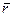/dt² = 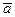– її прискорення, 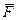– рiвнодiйна сил, прикладених до точки.

Рiвнiсть (3.1) називається основним диференцiальним рiвнянням руху матерiальної точки у векторнiй формi.

Координатна форма

Проектуємо рiвняння (3.1) на осi прямокутної декартової системи координат Oxyz:

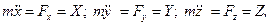(3.2)

де F_x,F_y,F_z - проекцiї сили на декартовi осi координат.

Рiвняння руху в цилiндричних координатах:

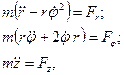(3.3)

де F_r, F_φ, F_z - проекцiї рiвнодiйної прикладених до точки сил на вiсi r, φ, z ( рис. 3.1 ).

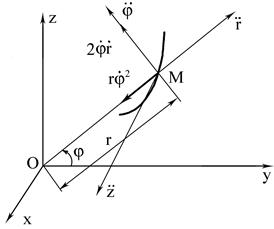
Рис. 3.1

Натуральна форма

Розкладаючи вектор прискорення на два компоненти по взаємно перпендикулярних напрямах дотичної i головної нормалi, одержимо:

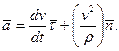(3.4)

В такому разi рiвняння руху в натуральнiй формi будуть мати вигляд:

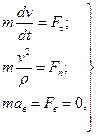(3.5)

де F_τ i F_n – проекцiї на додатно зорiєнтованi дотичну i головну нормаль рiвнодiйної 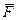сил, що дiють на точку (рис. 3.2).

Сила 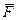i прискорення 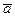точки завжди лежать у стичнiй площинi, орiєнтацiя якої в просторi визначається одиничними векторами 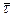i 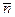. Проекцiя сили 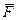на бiнормаль 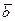дорiвнює нулю.

Рис. 3. 1.

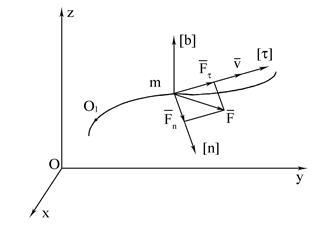
Рис. 3.2

§ 4. Двi основнi задачi динамiки точки. План їх розв’язання

У динамiцi матерiальної точки можна ставити i розв’язувати задачi двох основних типiв.

Перша основна задача.

Вiдомий закон руху матерiальної точки

r = r(t), (4.1)

треба визначити рiвнодiйну 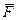сил, якi зумовили рух точки. Маса точки задається.

Спосiб розв’язування задачi: диференцiюємо двiчi рiвняння (4.1) i знаходимо прискорення 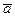(вiрнiше, його проекцiї). За диференцiальним рiвнянням руху знаходимо силу 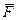або її проекцiї.

Друга основна задача (обернена).

Заданими є сила F = F(t, r, v) i ”початковi умови”: в певний (початковий) момент часу t₀ заданi радiус-вектор 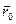i швидкiсть v₀ точки. Вiдома також маса точки. Треба знайти закон руху r = =r(t) точки в просторi.

Щоб розв’язати цю задачу, треба скласти диференцiальнi рiвняння руху i проiнтегрувати їх.

Момент часу t₀ називається початковим; положення точки, яке визначається радiус-вектором 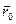, називається початковим положенням; швидкiсть точки в момент часу t₀ називається початковою швидкiстю v₀.

При розв’язуваннi задач динаміки матеріальної точки корисно додержуватись такого плану:

1) аналiз сил. Для цього треба:

а) видiлити дослiджуване тiло;

б) вказати усi навколишнi тiла, якi дiють на дослiджуване тiло;

в) визначити всi сили, що дiють на об’єкт дослiдження в русi вiдповiдно до тiл, перелiчених в пунктi б);

г) вказати залежнiсть сил вiд фiзичних параметрiв: часу, положення (координат), швидкостi i т. iн.;

2) показати на рисунку матерiальну точку (тiло) і прикладенi до неї заданi сили в довільний момент часу;

3) звiльнити точку вiд в’язей i показати сили реакцiй в’язей;

4) вибрати систему вiдлiку;

5) скласти диференцiальнi рiвняння руху матерiальної точки;

6) розв’язати складенi рiвняння руху;

7) проаналiзувати розв’язок.

Зауваження. Для закріплення матеріалу §§3-4 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М. Наука, 1981 (1986)“:

1) № 26.1, 26.2, 26.5, 26.6, 26.8; 27.1, 27.2, 27.4, 27.30, 27.40, 27.47;

2) № 26.9, 26.10, 26.13, 26.14, 26.17-26.20, 26.24, 26.26; 27.7, 27.9, 27.16, 27.17, 27.22, 27.26, 27.32, 27.37, 27.49, 27.54, 27.58;

3) № 26.31-26.35; 27.36, 27.38, 27.60, 27.61, 27.64, 27.65.

Рекомендується розв’язати також задачі № 8.3, 8.4, 8.6, 8.7, 8.8, 8.13, 8.15, 8.16, 8.18 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Питання для самоконтролю

1. Запишіть основне диференціальне рівняння руху матеріальної точки у векторній формі.

2. Як одержати диференціальні рівняння руху матеріальної точки в координатній формі? Напишіть ці рівняння.

3. Як записують рівняння руху матеріальної точки в циліндричних координатах?

4. Як одержати рівняння руху матеріальної точки в натуральній формі?

5. Поясніть розташування векторів рівнодійної сили 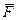і прискорення 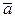при натуральні формі рівнянь руху матеріальної точки.

6. Сформулюйте першу задачу динаміки матеріальної точки.

7. Поясніть спосіб розв’язання першої задачі динаміки матеріальної точки.

8. Сформулюйте другу задачу динаміки матеріальної точки.

9. Опишіть методику розв’язання другої задачі динаміки матеріальної точки.

10. Які параметри називають початковими параметрами руху точки?

11. Сформулюйте загальний план розв’язання задач динаміки матеріальної точки.