IDEA NXT - новый подход в технологиях блочного симметричного шифрования
Ещё одно направление развития технологий блочного симметричного шифрования, которое заслуживает отдельного внимания - это, так называемое, ²гибкое шифрование², появившееся в связи с разработками, связанными с шифром FOX, задуманного в период 2001-2003 годов и опубликованного в 2004 году [34]. Этот шифр явился усовершенствованием европейского стандарта IDEA, который к тому времени уже прошел значительный период испытаний временем и обеспечил в течение всего этого периода задекларированный уровень стойкости. В мае 2005 года шифр FOX был анонсирован компанией MediaCrypt под названием IDEA NXT. Здесь напоминаются результаты анализа этого предложения, представленные в работе [35].
Сегодня, отмечается в этой работе, IDEA NXT выступает как универсальное семейство алгоритмов блочного симметричного шифрования, которое обеспечивает защиту электронных сред, данных, которые передаются в телекоммуникационных системах, и хранящихся данных. Семейство представлено набором двух модификаций шифров с различными размерами шифруемых блоков и ключей: Standard NXT64 (64-битный блок, 128-битный ключ, 12 раундов шифрования) и Standard NXT128 (128-битный блок, 256-битный ключ, 12 раундов шифрования). Могут также быть построены версии Standard с размерами ключей от 2-х до 256 битов и числами циклов от 2-х до 255. В шифрах предусмотрена загрузка индивидуальных таблиц (S-блоков и перестановочных матриц) для замены стандартных.
Главными особенностями (свойствами) этой разработки, как отмечается в публикациях, является высокий уровень защиты, высокая эффективность и беспрецедентный уровень гибкости реализации.
Как заявляет компания-собственник разработки, IDEA NXT имеет способность применения в динамической системе обновления, в результате чего защита может переустанавливаться после успешной атаки. Такая система позволяет пользователям (собственникам) и операторам осуществлять быстрое возвращение в нормальное рабочее состояние и продолжать поддерживать рентабельное производство без необходимости выполнения трудоёмкого аппаратного свопинга. IDEA NXT характеризуется гибким и масштабированным диапазоном операционных режимов, что позволяет динамично оптимизировать компромисс между эффективностью и безопасностью с одновременной поддержкой согласованности и эффективной функциональности в широком разнообразии устройств.
Математическая структура разработки построена на базе схемы Лея-Масея. В качестве табличных преобразований используются раундовые (цикловые) функции и элементы Замены-Перестановки (SPN). Кроме того, разработана новая структура стойких и эффективных алгоритмов разворачивания ключей.
IDEA NXT обеспечивает необходимый уровень управления настройками, включая простое и надёжное создание уникальных собственных версий алгоритмов. Такие версии создают дополнительную степень защиты для применений, которые требуют особенной обработки.
Кроме того:
- стандарт допускает эволюционную миграцию с существующими алгоритмами, такими как IDEA, AES и 3DES;
- настраиваемость позволяет заказчикам выбирать размеры ключей, число раундов для достижения компромиссного решения между эффективностью и степенью защищённости;
- заказной характер обеспечивает достижение максимального уровня защиты, с выдачей гарантийных уникальных таблиц, на базе которых создаётся собственный алгоритм;
- индивидуализация способствует адаптации IDEA NXT продукта к целевым процессорам или к заказанным сервисным требованиям.
Таким образом, судя по заявлениям компании-собственника разработки, предлагаемая технология обладает следующими преимуществами:
- высокий уровень защиты;
- высокая эффективность;
- гибкость и масштабируемость;
- разнообразие в применениях;
- динамическое обновление;
- настраиваемость для разных приложений;
- эволюционную миграцию с существующими алгоритмами;
- правовую защиту.
В [35] представлено краткое описание разработки, правда, не совсем аккуратное. Ниже приводятся некоторые уточнения.
Рассмотрим особенности проектных решений, принятых в IDEA NXT. Будем при этом ориентироваться на базовую конструкцию шифра FOX [34, 2004], лежащую в основе всех решений по построению семейства шифров IDEA NXT.
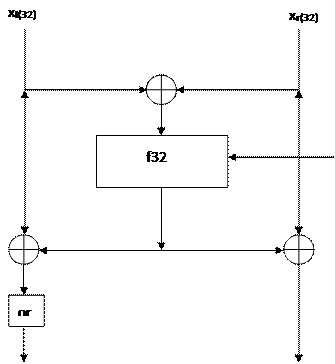
Напомним, что шифр FOX основан на схеме Лей-Месси [20,21, 1992, 1991]. Ее 64-битная реализация (Imor64) с дополнительным or преобразованием представлена на рис.1.2.
Сам шифр представляет собой r-1-разовое повторение функции Imor64. В конце процедуры шифрования выполняются функция Imid64. Она представляет собой слегка изменённую функцию Imor64 (отсутствует функция or).
 | |||
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
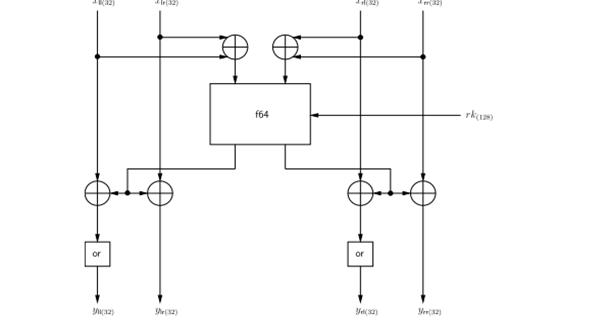
Рис. 1.3. Цикловая функция elmor128
Далее более подробно рассматривается реализации функций f32 и f64.
Функция f32 - ядро FOX64. Она состоит из комбинации трёх основных элементов: таблицы подстановок, рассеивающей части - mu4, и части сложения с цикловым ключом, образующих структуру, представленную на рис. 1.4.
Рассеивающая часть f32 представляет собой линейную 4´4 мультипере-становку в поле GF(28) [36], выполняемую с помощью матричного умножения:
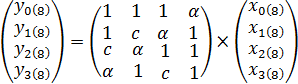 ,
,
где
с = α-1 + 1 = α6 + α5 + α4 + α3 + α2 + 1,
как и α - элементы поля GF(28), c порождающим полиномом
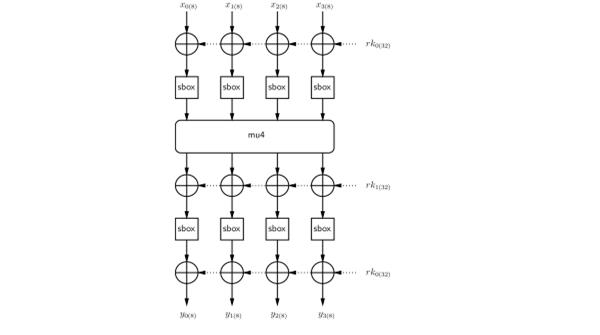
Рис. 1.4 Функция f32
P(α) = α8 + α7 + α6 + α5 + α4 + α3 + 1.
Функция f64, являющаяся ядром FOX128 [20, 21], состоит из комбинации тех же элементов, только удвоенных по численности (см. рис. 1.5).
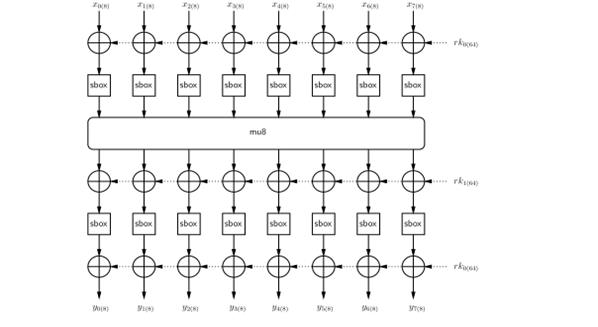
Рис. 1.5. Функция f64
mu8 - часть f64 в этом случае представляет собой линейную 8´8 мультиперестановку в поле GF(28) [37] и реализуется с помощью матричного умножения:
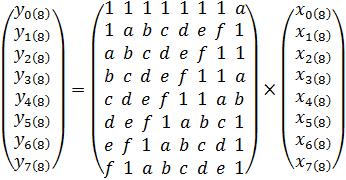 ,
,
где
a = α + 1,
b = α-1 + α-2 = α7 + α,
c = α,
d = α2,
e = α-1 = α7 + α6 + α5 + α4 + α3 + α2,
f = α-2 = α6 + α5 + α4 + α3 + α2 + α
- элементы поля GF(28). Умножение выполняются в поле GF(28), для которого снова используется порождающий полином
P(α) = α8 + α7 + α6 + α5 + α4 + α3 + 1.
Здесь стоит обратить внимание на то, что разработка шифра FOX велась уже после завершения конкурса AES, и, конечно же, авторы проекта знали о его результатах. Судя по представленным фрагментам конструкторских решений, получается, что проектировщики FOX-а включили в свою разработку одно из ключевых решений принятых при построении шифра Rijndael - конструкцию линейного преобразования, эффективно реализующего стратегию широкого следа.
Как показывает наш анализ, свойства шифрующего преобразования шифра FOX получились несколько лучше свойств шифрующего преобразования Rijndael (к асимптотическим показателям, свойственным случайной подстановке, шифр FOX выходит за три цикла (если не учитывать возможность пассивного прохода первого цикла), а шифр Rijndael за четыре).
Отдельного внимания заслуживает подход к построению нелинейного преобразования.
S-блоки шифра FOX.Разработчики S-блоков этого шифра [36]отмечают, что их первичная цель состояла в том, чтобы избежать чисто алгебраической конструкции для S-блока; вторичной целью стала возможность реализации S-блока эффективным путем в аппаратных средствах, использующих ASIC или FPGA технологии. Реализованная ими S-блоковая функция является нелинейным биективным отображением 8-ми битных входных значений в 8-ми битные выходные. Она строится с помощью схемы Лэя-Массэя [20] с тремя циклами, представленной на Рис. 1.6. Схема берет как цикловую функцию три разных "малых" (размером 4´4) подстановки и комбинирует с ними с помощью операций сложения по модулю два и ортоморфных преобразований, где ортоморфизм третьего цикла опущен.
Малые S-блоки обозначены S1, S2 и S3, а их содержимое приведено в табл. 1.1.
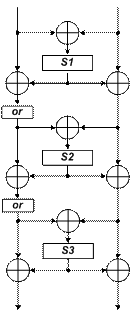
Рис.1.6. S-блок шифра FOX
Ортоморфизм or, использованный в схеме Лэя-Массэя, является одиночным циклом 4-х битовой схемы Фейстеля с цикловой функцией в виде функции тождества. Процесс формирования (выбора) S-блоковой конструкции состоял в следующем.Сначала псевдослучайным способом был выбран набор из трех кандидатов S1, S2 и S3 для малых подстановочных конструкций (S-блоков размера 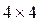 ).
).
Каждая из отобранных подстановок, представленных в табл. 1.1, имеет значения LPmax и DPmax не более чем 2-2 (обозначения из [34]), где
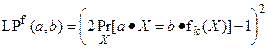 ,
,
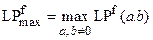 ,
,
с символом ·, обозначающим скалярное произведение двоичных векторов, и
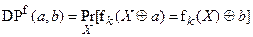 ,
,
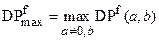 .
.
Таблица 1.1
Таблица нелинейных элементов замены S1(x), S2(x) и S3(x)
| x | ||||||||||||||||
| S1(x) | E | A | C | F | D | B | ||||||||||
| S2(x) | B | F | E | D | A | C | ||||||||||
| S3(x) | D | A | B | C | F | E |
В приведенных формулах LPmax и DPmax - максимальные (исключая первые входы в первую строку и первый столбец) значения линейной аппроксимационной таблицы и таблицы XOR разностей S-блока соответственно; a, b - битовые векторы соответствующей размерности, обозначающие маски входа и выхода (для LAT) либо входные и выходные разности для XOR таблицы XOR разностей, а X, 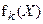 - вход и выход k-того
- вход и выход k-того
S-блока, выполняющего преобразование 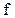 . DPmax соответствует понятию дифференциальной
. DPmax соответствует понятию дифференциальной  -равномерности S-блока, введенному еще в работах К. Нюберг.
-равномерности S-блока, введенному еще в работах К. Нюберг.
Затем кандидаты для итогового S-блока были оценены и протестированы относительно значений LPmax и DPmax до тех пор, пока хороший кандидат не был обнаружен. Авторы отмечают, что выбранный S-блок имеет показатели 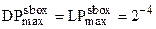 (для S-блока AES LPmax = DPmax = 2-6). Табл. 1.2 иллюстрирует свойства S-блока шифра FOX.
(для S-блока AES LPmax = DPmax = 2-6). Табл. 1.2 иллюстрирует свойства S-блока шифра FOX.
Конечно, по LPmax и DPmax показателям S-блок шифра FOX уступает
S-блоку AES. По остальным показателям случайности S-блок шифра FOX ни в чем существенно не отличается от показателей S-блоков многих других шифров. Однако и эти более низкие показатели позволяют, как показывается далее, обосновать разработчикам доказуемую стойкость шифра FOX к атакам дифференциального и линейного криптоанализа.
Центральное проектное решение - это конечно стойкость разработки.
Доказательство стойкости шифра FOX к атакам дифференциального и линейного криптоанализа осуществлено с использованием теоремы Hong-а и др. Сама теорема и излагаемая методика используется в большом числе других работ по оценке показателей стойкости шифров к атакам дифференциального и линейного криптоанализа. Поскольку у нас есть существенные претензии к чтобы продемонстрировать её сущность.
Таблица 1.2
Показатели случайности S-блока Fox
Analyzed substitution 8x8 [93 222 0..]
________________________________________________ _______ 5D DE 0 B7 D3 CA 3C D C3 F8 CB 8D 76 89 AA 12
88 22 4F DB 6D 47 E4 4C 78 9A 49 93 C4 C0 86 13
A9 20 53 1C 4E CF 35 39 B4 A1 54 64 03 C7 85 5C
5B CD D8 72 96 42 B8 E1 A2 60 EF BD 02 AF 8C 73
7C 7F 5E F9 65 E6 EB AD 5A A5 79 8E 15 30 EC A4
C2 3E E0 74 51 FB 2D 6E 94 4D 55 34 AE 52 7E 9D
4A F7 80 F0 D0 90 A7 E8 9F 50 D5 D1 98 CC A0 17
F4 B6 C1 28 5F 26 01 AB 25 38 82 7D 48 FC 1B CE
3F 6B E2 67 66 43 59 19 84 3D F5 2F C9 BC D9 95
29 41 DA 1A B0 E9 69 D2 7B D7 11 9B 33 8A 23 09
D4 71 44 68 6F F2 0E DF 87 DC 83 18 6A EE 99 81
62 36 2E 7A FE 45 9C 75 91 0C 0F E7 F6 14 63 1D
0B 8B B3 F3 B2 3B 08 4B 10 A6 32 B9 A8 92 F1 56
DD 21 BF 04 BE D6 FD 77 EA 3A C8 8F 57 1E FA 2B
58 C5 27 AC E3 ED 97 BB 46 05 40 31 E5 37 2C 9E
0A B1 B5 06 6C 1F A3 2A 70 FF BA 07 24 16 C6 61
_______________________________________________
Cycles: 8
Inversions: 17056
Increasing: 125
Max DT: 16
____________________
Number of max DT: 70
Max LAT: 32
Number of max LAT: 219
Elements DT:
0 42361
2 15377
4 5758
6 680
8 754
10 19
12 6
14 0
16 70
18 0
20 0
22 0
24 0
26 0
28 0
30 0
32 0
34 0
Elements LAT:
0 18686
2 0
4 18171
6 0
8 15888
10 0
12 6405
14 0
16 4280
18 0
20 983
22 0
24 352
26 0
28 41
30 0
32 219
В обозначениях работы [36] пусть S обозначает m×m подстановочный блок, который является биекцией над {0,1}m. Рассматривается стандартная kSPkSk структура (т.e. одна цикловая функция FOX-а) как слоистая конструкция из m×n битных строк, а именно слой сложения с ключом, подстановочный слой, диффузионный слой, следующий за ними второй слой ключевого сложения, подстановочный слой и заключительный слой с сложения с ключом. Полагается, что подстановочный слой состоит из n параллельно действующих m×m S-блоков S и для 1 ≤ i ≤ n, диффузионный слой может быть выражен как инвертируемая n×n MDS матрица M с коэффициентами из поля GF(2m), и что слой сложения с ключом состоит из поразрядного сложения по модулю два (XOR) mn-битного подключа с состоянием (блоком данных). Далее вводится обозначение 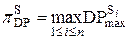 и
и 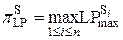 (максимальные дифференциальная и линейная вероятности S-блоков). Теперь можно привести теорему Hong-а и др. (здесь повторяется нумерация теорем из работы [36]).
(максимальные дифференциальная и линейная вероятности S-блоков). Теперь можно привести теорему Hong-а и др. (здесь повторяется нумерация теорем из работы [36]).
Теорема 3.3 (Hong и др.). В kSPkSk структуре, если цикловые ключи статистически независимы и распределены равномерно, то вероятность каждого дифференциала по отношению к операции Å ограничена сверху значением
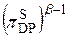 .
.
В то же время вероятность каждого линейного корпуса ограничена сверху значением
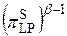 .
.
Здесь 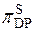 и
и 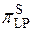 - максимальные значения таблицы дифференциальной разности и таблицы линейной аппроксимации S-блока соответственно, т.е. рассматривается методика оценки показателей стойкости шифров на основе привязки к дифференциальным и линейным свойствам
- максимальные значения таблицы дифференциальной разности и таблицы линейной аппроксимации S-блока соответственно, т.е. рассматривается методика оценки показателей стойкости шифров на основе привязки к дифференциальным и линейным свойствам
S-блоков входящих в шифр.
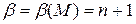 - число ветвлений диффузионного слоя M, которое определяется так, чтобы быть максимальным.
- число ветвлений диффузионного слоя M, которое определяется так, чтобы быть максимальным.
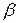 В случае FOX64, так как
В случае FOX64, так как 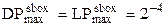 и функция mu4 (соотв. mu8) имеет число ветвлений равное пяти (соотв. 9), и так как можно предположить, что подключи равномерно распределены и статистически независимы, что должно быть естественным для алгоритма разворачивания ключей, можно, пишут авторы разработки, применить теорему 3.3. и получить следующий результат
и функция mu4 (соотв. mu8) имеет число ветвлений равное пяти (соотв. 9), и так как можно предположить, что подключи равномерно распределены и статистически независимы, что должно быть естественным для алгоритма разворачивания ключей, можно, пишут авторы разработки, применить теорему 3.3. и получить следующий результат
Теорема 3.4. Если цикловые подключи являются статистически независимыми и равномерно распределены, то справедлива следующая граница:
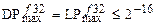
и
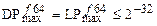 .
.
Далее доказываются леммы о том, что в расширенной схеме Лея-Массэя любая двухцикловая дифференциальная и линейная характеристики должны включать, по крайней мере, одну f64 функцию. И собирая теперь вместе приведенные теоремы и леммы, авторы приходят к утверждению
Теорема 3.5. Дифференциальная (соотв. линейная) вероятность любой однопутёвой характеристики в FOX64/k/r ограничена сверху значением 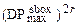 (соответственно
(соответственно 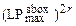 ). Подобно этому для FOX128/k/r верхней границей будет
). Подобно этому для FOX128/k/r верхней границей будет 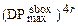 (соответственно
(соответственно 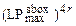 ).
).
Эти результаты позволяют авторам заключить, что невозможно обнаружить любой полезный дифференциал или линейную характеристику после восьми циклов и для FOX64 и для FOX128. Следовательно, минимальное число 12 циклов обеспечивает минимально безопасное значение.
Отметим здесь также, что в подобной же манере с использованием тщательных расчётов значений двухцикловых дифференциалов (и линейных аппроксимаций) выполнено обоснование доказуемых показателей стойкости шифра Rijndael (см., например, [37]).
Детальное изложение существующего подхода к оценке показателей стойкости шифров объясняется тем, что в дальнейшем будет доказано [см. также наши работы 38-41 и др.], что использованная авторами методика оценки средних значений максимумов переходов таблиц XOR разностей и смещений таблиц аппроксимаций (точнее максимумов средних значений), связываемая с дифференциальными и линейными показателями S-блоков, входящих в шифрующее преобразование, ошибочна. На самом деле итоговые показатели стойкости шифров к атакам дифференциального и линейного криптоанализа от S-блоков, применяемых в шифрах, не зависят. Поэтому приведенные разработчиками и исследователями обоснования и показатели стойкости нуждаются в пересмотре и уточнении.
В соответствии с развиваемой новой идеологией оценки показателей стойкости блочных шифров к атакам дифференциального и линейного криптоанализа, изложенной в нашей работе [41], рассмотренные шифры Rijndael, FOX и соответственно IDEA NXT имеют при одинаковых размерах битовых входов одинаковые показатели стойкости.
Представленный анализ принципов проектирования современных шифров позволяет выделить следующие существенные результаты:
1. Безусловным достижением современных конструкторских решений по построению шифров следует считать реализацию стратегии широкого следа, строящуюся на основе матричного умножения в расширениях полей.
2. Заслуживают одобрения и поддержки принципы проектирования, применённые разработчиками AES-а такие как:
- простота спецификации и простота анализа;
- прозрачность;
- эффективность.
2. Пропагандируемая новая концепция гибкого шифрования безусловно является шагом вперёд в технологиях блочного симметричного шифрования и при желании легко может быть реализована с использованием многих других разработок, а не только с помощью семейства шифров IDEA NXT.
3. Приведенные в публикациях подходы и результаты оценки показателей стойкости к атакам дифференциального и линейного криптоанализа не являются объективными и нуждаются в уточнении.
4. Сегодня уже существует подход, позволяющий вычислительным путем определить показатели стойкости блочных симметричных шифров к атакам дифференциального и линейного криптоанализа. В соответствии с этим подходом шифры семейства IDEA NXT по своим показателям стойкости находятся на уровне показателей стойкости, реализуемых многими другими шифрами, т.е. рассмотренная разработка в этом отношении не имеет заметных преимуществ по сравнению со многими другими (здесь имеются в виду и шифры, представленные на украинский конкурс).
5. Структура Лэя-Массэя (архитектура верхнего уровня) не создаёт сколько-нибудь ощутимых преимуществ по сравнению с конструкцией цикловой функции, применённой в шифре Rijndael.
6. Представляется, что одним из дополнительных проектных решений в перспективных разработках должно стать использование цикловой функции с высокими динамическими характеристиками перехода к установившимся (стационарным) значениям максимумов полных дифференциалов и линейных корпусов.
[1] Сейчас уже выполненными нами исследованиями малых моделей шифров показано, что показатели стойкости шифра Rijndael к линейному и дифференциальному криптоанализу от свойств S-блоков не зависят.
[2] число ветвлений B (BL -линейное и BD - дифференциальное) - нижняя граница для числа активных S-блоков в смежных циклах для дифференциальной или линейной характеристики.
Дата добавления: 2016-09-26; просмотров: 3221;











