Формула полной вероятности
Вероятность события А, которое может наступить лишь при условии появления одного из n попарно несовместимых событий В1, В2, ..., Вn образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Р (А) = Р (В1) PB1 (А) + Р (В2)РВ2 (А) + ... + Р (Вn)РBn(А)
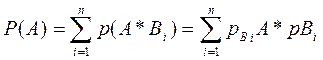
Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором — три белые и одна серая, в третьем — две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?
Обозначим В1 — выбор первого ящика, В2 — выбор второго ящика, B3 — выбор третьего ящика, А — извлечение белой мыши.
Так как все ящики одинаковы, то Р (B1)= Р (B2) = Р (B3) = 1/3.
Если выбран первый ящик, то Рв1 (А) = 2/3. Аналогично Рв2 (А) =3/4, Рв3(А) = 0,5. Наконец, по формуле получаем:
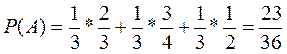
В группе студентов 4 отличника, 13 хорошо успевающих и 8 слабых студентов. Результаты предшествующих экзаменационных сессий показали, что отличники получают только отличные оценки (потому они и отличники); «хорошисты», как правило, в девяти случав из десяти получают отличные или хорошие оценки; наконец слабые студенты в одном случае из пяти получают хорошие оценки.
Для сдачи экзамена выбирается один студент. Найти вероятность события А, что студент получит хорошую или отличную оценку.
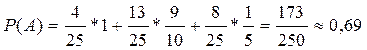
Дата добавления: 2020-10-01; просмотров: 679;











