Ортогональное проецирование прямой линии

4.1. Общие понятия и определения. Прямая в пространстве и на ортогональном чертеже может быть задана: а) двумя точками; б) точкой и направлением прямой; в) двумя пересекающимися плоскостями.

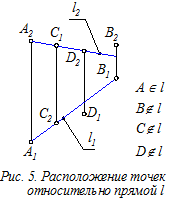
Определение. На эпюре точка лежит на прямой, если её проекции расположены на одноимённых проекциях этой прямой (рис. 5).

4.2. Расположение прямой относительно плоскостей проекций

В рассматриваемом разделе производится оценка проекционных свойств прямых в зависимости от их расположения относительно плоскостей проекции П₁, П₂ и П₃. При этом прямые в основном задаются лишь двумя своими проекциями (горизонтальной и фронтальной).

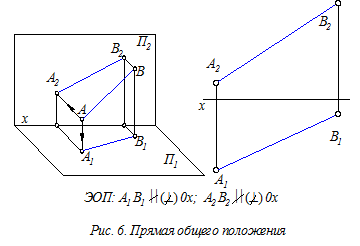Прямая общего положения – это прямая, не перпендикулярная ни одной из плоскостей проекций (П₁, П₂ или П₃). Эпюрный опознавательный признак (ЭОП) прямых общего положения – обе заданные проекции прямых непараллельны и неперпендикулярны к координатным осям (рис. 6).

Проекционные свойства (ПС) прямых общего положения – длина прямых и углы их наклона к плоскостям проекций на ортогональном чертеже искажены, т. е. показаны не в натуральную величину.

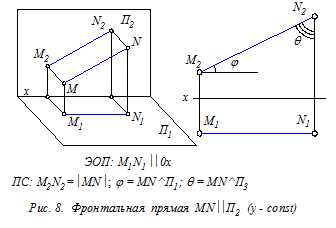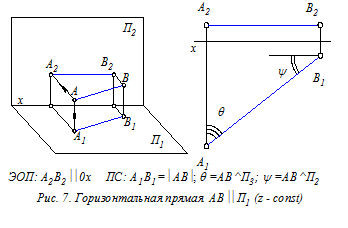
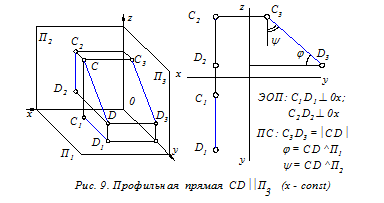
Прямые уровня (рис. 7 - 9) – это прямые, расположенные параллельно одной из плоскостей проекций (П₁, П₂ или П₃). ПС прямых уровня: на указанную плоскость проекций такие прямые отображаются в натуральную величину. Кроме этого на эту плоскость без искажения проецируются и углы наклона прямых к двум другим плоскостям проекций.

ЭОП прямых уровня: одна из заданных проекций прямой уровня параллельна координатной оси (0х или 0z). Это означает, что одна из трёх координат любой точки прямой уровня постоянна (т.е. не изменяется).

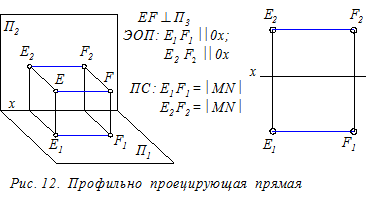
Прямые проецирующие – это прямые, расположенные перпендикулярно одной из плоскостей проекций (П₁, П₂ или П₃). На указанную плоскость такие прямые проецируются вырожденно, в виде точки (рис.10 - 12). На две другие плоскости проекций прямые отображаются в натуральную величину, т. к. они параллельны этим плоскостям.

Определение. Вырожденной проекцией прямой называется точка ортогонального чертежа, где отобразились все точки этой прямой.

Вырожденная проекция прямойобладает собирательным свойством: проекции всех точек прямой расположены в одной точке чертежа.

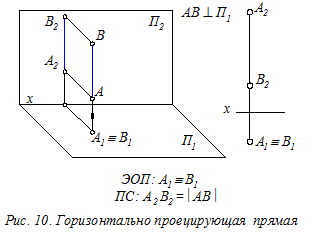
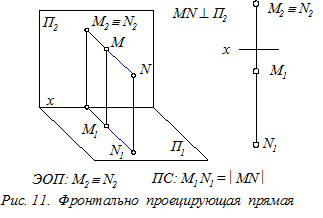
Прямые уровня и проецирующие прямые называются прямыми частного положения.

Рассмотрев различные положения прямой относительно плоскостей проекций можно сформулировать следующее правило:

Если на ортогональном чертеже (эпюре) одна из двух заданных проекций прямой параллельна координатной оси или вырождается в точку, то на другой проекции прямая отобразилась в натуральную величину.