Ортогональное проецирование точки на три плоскости проекций

Рассмотрим три взаимно перпендикулярные плоскости проекций:

П₁ – горизонтальная, П₂ – фронтальная и П₃ – профильная, пересечение которых образует прямоугольную систему координат 0xyz (рис. 3).

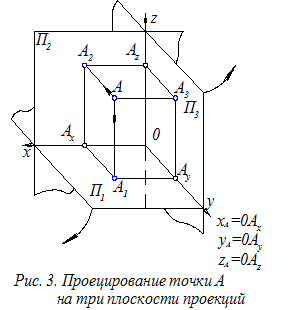Определение. Ортогональной проекцией точки А на плоскость проекций П₁ называется основание перпендикуляра (А₁), проведённого из точки А на указанную плоскость проекций.

Выполнив проецирование точки А на все три плоскости П₁, П₂ и П₃, получим соответственно горизонтальную (А₁), фронтальную (А₂) и профильную (А₃) проекции точки А.

Если спроецировать точку А на координатные оси 0x, 0y, 0z (точки А_x, А_y, A_z соответственно), то можно определить координаты точки А в рассматриваемой системе. Такими координатами будут отрезки: х_А=0А_х, у_А=0А_У, z_A=0A_z.

В рассматриваемом случае точка А(х_А, y_А, z_А) пространства имеет проекции А₁(х_А, y_А),
А₂(х_А, z_А), А₃(y_А, z_A), каждая из которых содержит две из трёх координат точки. Из этого рассмотрения следует вывод:

Любые две ортогональные проекции точки однозначно определяют положение точки в пространстве и на чертеже, т.к. используют все три координаты точки.

Поэтому в дальнейшем, при решении задач НГ геометрические фигуры будут задаваться двумя своими проекциями.

Кроме этого отметим геометрический смысл прямоугольных координат точки:

Координата точки определяет удаление этой точки от соответствующей плоскости проекций (например, координата z_А – удаление точки А от плоскости П₁, координата у_А – это удаление точки А от плоскости П₂, , а координата х_А - от плоскости П₃).

Если точка имеет одну нулевую координату, то она лежит на одной из плоскостей проекции. Если точка имеет две нулевые координаты, то она лежит на одной из координатных осей.

Переход от пространственной модели проецирования точки А (см. рис. 3) к её ортогональному чертежу (эпюру) – рис. 4 осуществляется путём совмещения в единую плоскость трёх плоскостей проекций П₁, П₂ и П₃. (плоское преобразование Г. Монжа) При этом на эпюре не присутствует геометрический объект - точка А, но показываются её проекции.

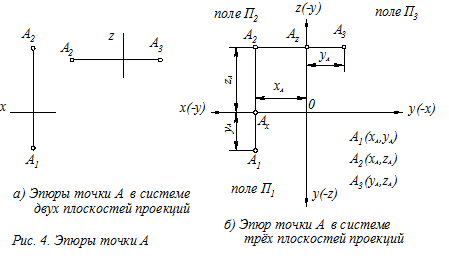Определение. Эпюром (ортогональным чертежом) точки называется изображение, содержащее две проекции точки, расположенные на линии связи, перпендикулярной координатной оси (рис. 4, а)

При переходе от пространственной модели проецирования точки А к её эпюру в системе трёх плоскостей проекций (рис. 4,б) надо иметь ввиду следующие обстоятельства:

1. Каждая и координатных осей является наложением двух осей.

2. Координата точки А на эпюре определяется расстоянием от проекции точки до соответствующей координатной оси (см. рис. 4).