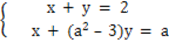В) Уравнение прямой с угловым коэффициентом.

Уравнение прямой.

Уравнение прямой можно записать несколькими способами.
Рассмотрим три из них:

А) Общее уравнение прямой.

Уравнение Ax+By+C=0 называется общим уравнением прямой на плоскости.

Таким образом, заданному уравнению вида Ax+By+C=0 соответствует прямая на плоскости в данной системе координат, а прямой линии на плоскости в данной системе координат соответствует уравнение прямой вида Ax+By+C=0 .
Общее уравнение прямой называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным. Неполное уравнение прямой вида Ax+By+C=0 определяют прямую, проходящую через начало координат. При А=0 уравнение Ax+By+C=0 задает прямую, параллельную оси абсцисс Ox, а при В=0 – параллельную оси ординат Oy.


Б) Уравнение прямой в отрезках.


Уравнение прямой вида x/a+y/b=1, где a и b – некоторые действительные числа, отличные от нуля, называется уравнением прямой в отрезках. Это название не случайно, так как абсолютные величины чисел а и b равны длинам отрезков, которые прямая отсекает на координатных осях Ox и Oy соответственно (отрезки отсчитываются от начала координат).

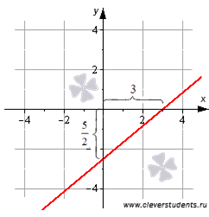
Пример: График прямой, заданной уравнением x/3+у/(-2,5)=1

 

В) Уравнение прямой с угловым коэффициентом.

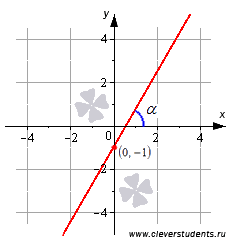
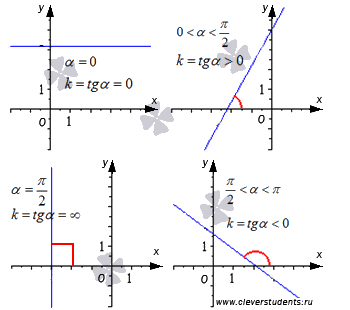
  Уравнение прямой вида kx+b=y, где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент).   Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, .  


На рисунке показан угол наклона прямой и указано значение углового коэффициента при различных вариантах расположения прямой относительно прямоугольной системы координат.


2. Расстояние между точками.
Формула вычисления расстояния между двумя точками A(xa, ya) и B(xb, yb) на плоскости:

AB = √((xb - xa)2 + (yb - ya)2)

 

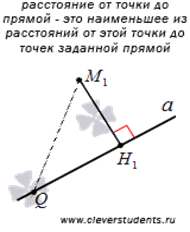
Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M1, не лежащая на прямой a. Проведем через точку M1 прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H1. Отрезок M1H1 называется перпендикуляром, проведенным из точки M1 к прямой a.  
3. Расстояние от точки до прямой.

4. Алгоритм для нахождения расстояния
от заданной точки 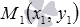до заданной прямой:

· находим общее уравнение прямой a вида 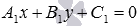или уравнение прямой a с угловым коэффициентом ;

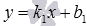  • получаем общее уравнение прямой b вида 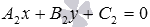или уравнение прямой b с угловым коэффициентом вида 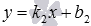, учитывая, что прямая b проходит через заданную точку M1 и перпендикулярна заданной прямой a;
  • определяем координаты 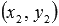точки H1 - точки пересечения прямых a и b, решая систему линейных уравнени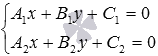й или ;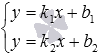

  • вычисляем требуемое расстояние от точки M1 до прямой a по формуле .

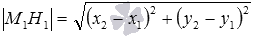5. Вспомним возможные случаи расположения прямых на координатной плоскости:

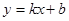
ax + by + c = 0,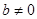
Две прямые могут:
- пересекаться в одной точке ( )
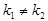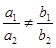
- быть параллельными ( )
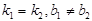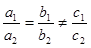
- совпадать (k1 = k2, b1 = b2)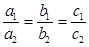
- быть перпендикулярными (k1 k2 = -1)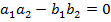    

 

Замечание(!)
Таким образом, если система линейных уравнений имеет одно решение, это значит, что две прямые, заданные этими уравнениями, пересекаются в одной точке.


Если система не имеет решений, то прямые не пересекаются, то есть являются параллельными.
Если система линейных уравнений, задающая две прямые, имеет бесконечное кол-во корней, то прямые совпадают.


Если помнить, что происходит с коэффициентами прямых в зависимости от их взаимного положения, можно легко решать следующие задачи с параметром J

Пример 1.
Найти все значения для параметра а, при которых система уравнений не имеет решений.

 
 



Решение.
Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а1 = b/b1 ≠ c/c1). Тогда имеем:

1/1 = (а2 – 3)/1 ≠ а/2 или систему

 

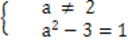
Из первого уравнения а2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.
Ответ: а = -2.

 

!! Повторите способы решения систем линейных уравнений, а также способы решения неравенств.
Все это пригодится на маленькой самостоятельной работе (Летучке) на занятии 26 октября.
<== предыдущая лекция | следующая лекция ==>
Энергия. Потенциальная и кинетическая энергия. Закон сохранения энергии. | Общие сведения об операционной системе Windows

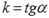Дата добавления: 2016-11-04; просмотров: 5185;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.01 сек.