Компартментальные модели

В простейших структурированных моделях предусматривается компартментация биомассы в небольшом числе компонентов. Иногда эти компоненты имеют приближенное биохимическое толкование, например синтетический компонент (РНК и предшественники) и структурный компонент (ДНК и белки). Компартменты могут быть также определены как ассимилирующий компонент и синтетический компонент. В другой интерпретации при создании простых компартментальиых моделей используется понятие об узких местах метаболизма.

Использование структурированных моделей с небольшим числом переменных оправданно также с точки зрения некоторых принципов динамики систем. Каждый тип реакций и транспортных явлений, осуществляющихся в популяции клеток (молекулярные соударения, химические реакции, диффузия, кругооборот РНК, синтез белков, увеличение числа клеток, завершение периодического процесса, спонтанные мутации), характеризуется своим временем релаксации, т. е. временем, необходимым для перехода в стационарное состояние после возмущения (вспомните разд. 3.1). Время релаксации может изменяться от долей секунды до нескольких часов. С точки зрения динамики систем в моделировании наиболее важна взаимосвязь между диапазоном времени, в течение которого совершаются изменения в среде (хе), и спектром времен релаксации внутриклеточных процессов. Можно допустить, что клеточные процессы, характеризующиеся быстрой реакцией на изменения в среде (те. небольшой величиной отношения времени релаксации к хе), находятся в квазистационарном состоянии (разд. 3.2.1). В другом крайнем случае, когда время релаксации некоторых клеточных процессов велико по сравнению с хе, эти клеточные процессы можно считать «замороженными» в начальном состоянии. Примером могут служить глубокие генетические изменения, которые практически никогда не осуществляются в ходе одного периодического процесса.

Установлено, что в случае многих сложных систем только два или три времени релаксации находятся в том же временном диапазоне, что и изменения в среде; этот факт еще раз: подтверждает обоснованность приближенного описания динамики сложных систем с помощью упрощенной модели с двумя или тремя переменными. В то же время часто трудно или даже невозможно связать некоторые из этих переменных с измеряемыми физическими количественными характеристиками системы. Ниже мы рассмотрим некоторые примеры простых компартментальных кинетических моделей роста клеточной популяции.

Уильяме предложил двукомпартментальную модель, которая удивительно точно описывает некоторые стороны динамики клеточного роста в периодическом процессе [16]

Основные постулаты этой модели формулируются следующим образом:

1. Синтетический компонент (1) продуцируется в результате поглощения внешнего питательного вещества S с экономическим коэффициентом У (отношение массы компонента 1 к массе субстрата). Реакция образования синтетического клеточного компонента имеет первый порядок по общей плотности клеток х (отношению клеточной массы к объему культуры) и по массовой концентрации питательного вещества (отношению массы субстрата к объему культуры).

2. Структурно-генетический компонент клетки (2) продуцируется из компонента 1 со скоростью, пропорциональной p₁p₂ (р_i — отношение массы i к единице объема клеток).

3. Для деления клетки необходимо и достаточно удвоение компонента 2. Следовательно, численная плотность клеток пропорциональна концентрации компонента 2 в культуре.

4. Биомасса построена только из компонентов 1 и 2.

Для реактора периодического действия при условии полного (перемешивания эти же постулаты можно выразить в математической форме:

где f₂ = p₂/p_c представляет собой долю клеточной массы, состоящей из компонента 2. С помощью двух уравнений этой модели s можно выразить через х. Если таким путем преобразовать уравнение (7.69), то мы получим выражение, по форме совпадающее с уравнением (7.51). Следовательно, изменение х будет подчиняться логистическому уравнению типа (7.52).

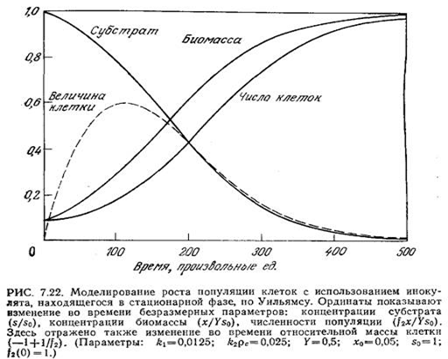
Предложенный Уильямсом подход применялся для моделирования роста популяции клеток в периодическом процессе с использованием инокулята, находящегося в стационарной фазе в среде с истощенным питательным веществом, что соответствует p₁ = 0. Полученные таким путем результаты приведены на рис. 7.22; они хорошо воспроизводят некоторые часто наблюдаемые на практике особенности роста культур микроорганизмов в периодическом процессе, включая:

1. Лаг-фазу, в течение которой возрастают размеры клеток.

2. Фазу экспоненциального роста, в которой размер клеток достигает максимума.

3. Изменения в составе клеток в цикле роста. Поскольку такие изменения, очевидно, происходят даже в экспоненциальной фазе, отсюда следует, что рост клеток идеально не сбалансирован ни в одной из фаз роста.

4. Стационарную фазу с относительно небольшими клетками. Обратите особое внимание на то, что изменения во времени плотности популяции по массе и по численности клеток непропорциональны; иными словами, масса индивидуальной клетки зависит от скорости роста и даже от предыстории скорости роста. Аналогичные результаты были получены в ходе детального изучения роста популяций Е. coli и 5. cerevisiae [30, 31]. Приведенные данные свидетельствуют о том, что динамику изменений клеточной массы часто можно описать с достаточно хорошим приближением относительно простыми математическими моделями; напротив, расчеты динамики численности популяции более сложны.