Неструктурированные модели клеточного роста в периодических процессах

В простейшем подходе к моделированию роста культуры клеток в периодическом процессе мы допускаем, что скорость роста клеточной массы во времени является функцией одной лишь клеточной массы, т. е.

Как мы скоро увидим, из этого уравнения отнюдь не следует, что мы должны пренебрегать любыми изменениями, происходящими в ходе клеточного роста в среде.

Одной из простейших моделей типа (7.49) является закон Мальтуса, который математически можно выразить следующим образом: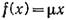

где µ — константа. Нетрудно видеть, что таким же образом выражается уже известная нам закономерность накопления клеточной массы в фазе экспоненциального роста. Предсказание Мальтуса о неизбежности рокового конца человечества в результате неконтролируемого роста народонаселения не оправдалось (или, быть может, пока еще не оправдалось?); так же и в случае популяций микроорганизмов вслед за фазой экспоненциального роста наблюдается переход к стационарной популяции.

Эта теория получила дальнейшее развитие в работах Ферлхурста (1844 г.), а также Перла и Рида (1920 г.), которые при анализе роста популяции стали учитывать ингибирующий фактор. Допустив, что ингибирование пропорционально х², эти исследователи предложили уравнение

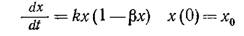
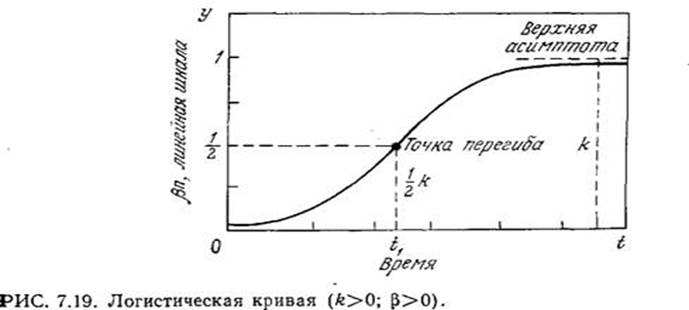
Это выражение представляет собой уравнение Риккати; его интегрирование не представляет затруднений и приводит к уравнению логистической кривой:

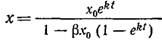
Как показано на рис. 7.19, логистическая кривая имеет S-образную форму и приводит к стационарной популяции с максимальной концентрацией биомассы x_s=l/β.

Одно из возможных объяснений логистической кривой сводится к допущению, что скорость продуцирования токсина пропорциональна скорости роста популяции:

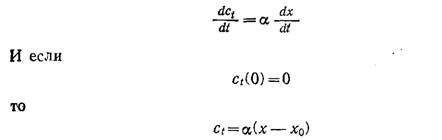
Обычно пренебрежимо мало по сравнению с x; в таких случаях подстановка уравнения (7.55) в (7.42) приводит к уравнению типа (7.51).

Описанные выше неструктурированные модели клеточного роста имеют несколько недостатков. В частности, в них не находит отражения лаг-фаза, не учтены влияющие на рост клеток различные переменные, а также данные о метаболизме клетки и его регуляции. В последующих разделах мы попытаемся найти связи между сложной биохимией клетки и явлениями, наблюдаемыми при росте популяции в периодическом процессе.