Структурированные модели кинетики клеточного роста

Неструктурированные модели описывают только количество биологической фазы. Такие модели не учитывают и никоим образом не отражают состав биофазы, т. е. то, что можно назвать ее качественными характеристиками. Если в процессе роста существенно изменяется состав клеточной популяции и если это изменение влияет на кинетику клеточного роста, то анализ таких систем возможен только с помощью структурированных моделей. Поскольку ни в одной модели практически невозможно учесть материальные балансы всех компонентов клетки, то при создании структурированной модели (по необходимости приближенной) мы, очевидно, должны тщательно отобрать ключевые переменные и процессы, играющие важнейшую роль в планируемом применении этой модели. Как мы покажем на ряде примеров в следующих разделах, структурированные модели могут быть построены на основе различных концепций.

В структурированных моделях в качестве переменных биофазы обычно применяются массовая (x_j) или молярная (с_j) концентрации в единице объема биофазы [15]. При условии полного перемешивания уравнение материального баланса по компоненту j можно записать в следующем виде:

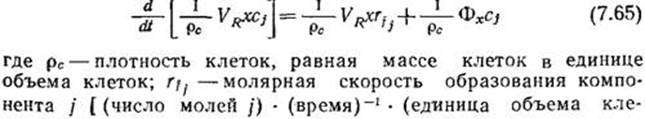
ток)^-1; Ф_х – масса клеток, вводимых в реактор в единицу времени; V_R – объем культуры; х - концентрация клеточной массы [(масса клеток) (единица объема культуры)^-1] c_j – (число молей j) (единица объема клеток)^-1]. В последнем слагаемом уравнения (7.65) принимается, что вводимые в реактор (например, в рецикле) или выводимые из реактора клетки находятся в том же состоянии, что и популяции клеток в реакторе. Если это условие не выполняется (например, во втором или одном из последующих реакторов в каскаде ПРПП), то уравнение баланса должно быть соответствующим образом модифицировано.

Если допустить, что плотность клеток р_с и объем культуры V_R не изменяются во времени, то после дифференцирования уравнения (7.65) получим

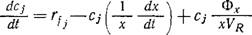(7.66)

Для реактора периодического действия Фх равно нулю, а выражение в скобках в правой части уравнения (7.66) есть не что иное, как удельная скорость роста µ; следовательно, для этого случая уравнение (7.66) преобразуется следующим образом:

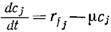(7.67)

Физический смысл r_f. ясен; выражение - µс_j отражает снижение концентрации, обусловленное разведением в процессе роста популяции клеток. Интересно, что оценка правой части уравнения (7.66) для ПРПП при стерильности питательных веществ опять-таки приводит к уравнению (7.67).