Расчёты на жесткость при изгибе

Пример 6. Определить прогиб двутавровой балки № 30 (ГОСТ 8239—72) пролетом l = 6 м, нагруженной равномерно распределенной по всему пролету нагрузкой интенсивностью q = 20 Н/мм.

Решение

Абсолютная величина прогиба определяется по формуле:

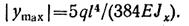
Принимая Е = 2,0_*10⁵ Н/мм² и J_x = 7080_*10⁴ мм⁴ (по таблице ГОСТ)., получаем

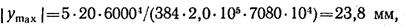
что составляет 1/251 пролета

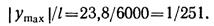
Пример 7. Подобрать сечение стальной двутавро­вой балки пролетом 4,8 м, нагруженной равномерно рас­пределенной по всему пролету нагрузкой интенсивностью q = 5 кНм = 5 Н/мм и сосредоточенной силой Р = 30 кН, приложенной посередине пролета, исходя из условий прочности и жесткости, если допускаемое напряжение [σ] = 140 Н/мм², а допускаемый прогиб [f/l] = 1/600. При­нять E = 2,1 • 10⁵ Н/мм².

Решение

Наибольший изгибающий момент при задан­ном нагружении

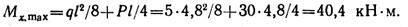
Требуемый момент сопротивления по условию проч­ности

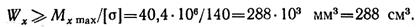
Ближайший по ГОСТ 8239—72 двутавр № 24 имеет W_x = 289 см³.

Абсолютная величина наибольшего прогиба посередине пролета определяется как сумма прогибов для каждого из двух нагружений:

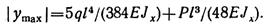
По условию жесткости он не должен превышать 1/600 пролета. Имеем

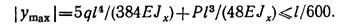
Сократив на l и подставив числовые значения, получим

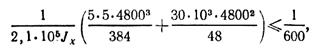
откуда требуемый момент инерции сечения

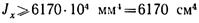
Двутавр № 24 имеет J = 3460 см⁴ и недостато­чен для обеспечения жест­кости балки. Следует при­нять двутавр № 30 с J_x = 7080 см⁴.

Пример 8. Проверить жесткость балки, изображен­ной на рис. 2.63, если угол поворота ее свободного конца не должен превышать 1°; принять Е = 2,0*10⁴ Н/мм².

Решение

Момент инерции заданного сечения балки

Полный угол поворота свободного конца В опреде­лится как сумма углов поворота от каждой из трех на­грузок, при этом учтем, что 100 Н/м=0,1 Н/мм:

Жесткость балки недостаточна.