Особенность расчета валов
Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольцевым сечением. При расчете валов касательные напряжения от действия поперечных сил не учитывают из-за их незначительности.
Расчеты проводят по опасным поперечным сечениям. При пространственном нагружении вала пользуются гипотезой независимости действия сил и изгибающие моменты рассматривают в двух взаимно перпендикулярных плоскостях, а суммарный изгибающий момент определяют геометрическим суммированием.
Примеры решения задач
Пример 1. В опасном поперечном сечении круглого бруса возникают внутренние силовые факторы (рис. 35.1) Мх; Му; Mz.
Мх и Му — изгибающие моменты в плоскостях уОх и zOx соответственно; Mz — крутящий момент. Проверить прочность по гипотезе наибольших касательных напряжений, если [σ] = 120 МПа. Исходные данные: Мх = 0,9 кН • м; Му = 0,8 кН • м; Mz = 2,2 кН*м; d = 60 мм.
Решение
Строим эпюры нормальных напряжений от действия изгибающих моментов относительно осей Ох и Оу и эпюру касательных напряжений от кручения (рис. 35.2).
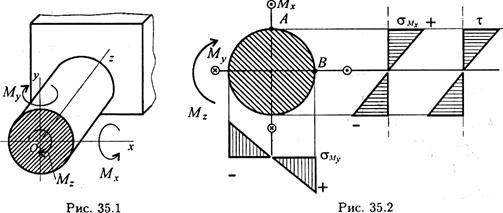
Максимальное касательное напряжение возникает на поверхности. Максимальные нормальные напряжения от момента Мх возникают в точке А, максимальные нормальные напряжения от момента Му в точке В. Нормальные напряжения складываются, потому что изгибающие моменты во взаимно перпендикулярных плоскостях геометрически суммируются.
Суммарный изгибающий момент:
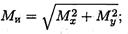
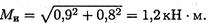
Рассчитываем эквивалентный момент по теории максимальных касательных напряжений:
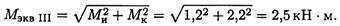
Условие прочности:
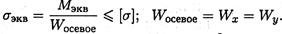
Момент сопротивления сечения: Woceвoe = 0,1 • 603 = 21600мм3.
Проверяем прочность:
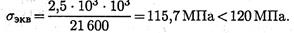
Прочность обеспечена.
 Пример 2. Из условия прочности рассчитать необходимый диаметр вала. На валу установлены два колеса. На колеса действуют две окружные силы Ft1 = 1,2кН; Ft2 = 2кН и две радиальные силы в вертикальной плоскости Fr1 = 0,43кН; Fr2 = 0,72кН (рис. 35.3). Диаметры колес соответственно равны d1 = 0,1м; d2 = 0,06 м.
Пример 2. Из условия прочности рассчитать необходимый диаметр вала. На валу установлены два колеса. На колеса действуют две окружные силы Ft1 = 1,2кН; Ft2 = 2кН и две радиальные силы в вертикальной плоскости Fr1 = 0,43кН; Fr2 = 0,72кН (рис. 35.3). Диаметры колес соответственно равны d1 = 0,1м; d2 = 0,06 м.
Принять для материала вала [σ] = 50МПа.
Рассчитать размеры вала кольцевого сечения при с = 0,8 (с = dвн / d).
Расчет провести по гипотезе максимальных касательных напряжений. Весом вала и колес пренебречь.
Решение
Указание. Используем принцип независимости действия сил, составляем расчетные схемы вала в вертикальной и горизонтальной плоскостях. Определяем реакции в опорах в горизонтальной и вертикальной плоскостях в отдельности. Строим эпюры изгибающих моментов (рис. 35.4). Под действием окружных сил вал скручивается. Определяем действующий на валу крутящий момент.
Составим расчетную схему вала (рис. 35.4).
1. Крутящий момент на валу:
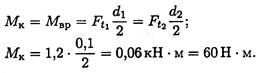
2. Изгиб рассматриваем в двух плоскостях: горизонтальной (пл. Н) и вертикальной (пл. V).
В горизонтальной плоскости определяем реакции в опоре:
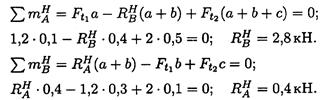
Определяем изгибающие моменты в точках С и В:

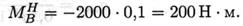
 |
В вертикальной плоскости определяем реакции в опоре:
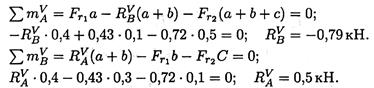
Определяем изгибающие моменты в точках С и В:
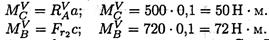
Суммарные изгибающие моменты в точках С и В:
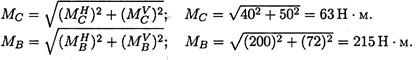
В точке В максимальный изгибающий момент, здесь же действует и крутящий момент.
Расчет диаметра вала ведем по наиболее нагруженному сечению.
3. Эквивалентный момент в точке В по третьей теории прочности
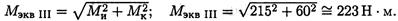
4. Определяем диаметр вала круглого поперечного сечения из условия прочности
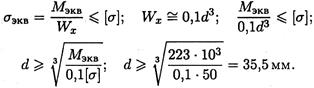
Округляем полученную величину: d = 36 мм.
Примечание. При выборе диаметров вала пользоваться стандартным рядом диаметров (Приложение 2).
5. Определяем необходимые размеры вала кольцевого сечения при с = 0,8, где d — наружный диаметр вала.



Диаметр вала кольцевого сечения можно определить по формуле
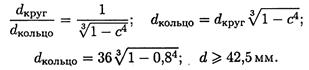
Примем d = 42 мм.
Перегрузка незначительная. dBH = 0,8d = 0,8 • 42 = 33,6мм.
Округляем до значения dBH = 33 мм.
6. Сравним затраты металла по площадям сечения вала в обоих случаях.
Площадь поперечного сечения сплошного вала
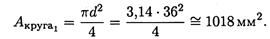
Площадь поперечного сечения полого вала

Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения:
Пример 3. Определить размеры поперечного сечения вала (рис. 2.70, а) привода управления. Усилие от тяги педали P3, усилия, передаваемые механизмом P1, Р2, Р4. Материал вала — сталь СтЗ с пределом текучести σт = 240 Н/мм2, требуемый коэффициент запаса [n] = 2,5. Расчет выполнить по гипотезе энергии формоизменения.
Решение
Рассмотрим равновесие вала, предварительно приведя силы Р1, Р2, Р3, Р4 к точкам, лежащим на его оси.
Перенося силы Р1 параллельно самим себе в точки К и E, надо добавить пары сил с моментами, равными моментам сил Р1 относительно точек К и Е, т. е.
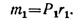
Эти пары сил (моменты) условно показаны на рис. 2.70, б в виде дугообразных линий со стрелками. Аналогично при переносе сил Р2, Р3, Р4 в точки K, E, L, Н надо добавить пары сил с моментами
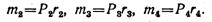
Опоры вала, изображенного на рис. 2.70, а, надо рассматривать как пространственные шарнирные опоры, препятствующие перемещениям в направлении осей х и у (выбранная система координат показана на рис. 2.70, б).
Пользуясь расчетной схемой, изображенной на рис. 2.70, в, составим уравнения равновесия:
 |
 |
Составим проверочное уравнение:
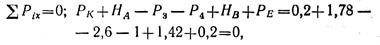
следовательно, опорные реакции НА и НВ определены верно.
Эпюры крутящих моментов Мz и изгибающих моментов Му представлены на рис. 2.70, г. Опасным является сечение слева от точки L.
Условие прочности имеет вид:
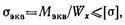
где эквивалентный момент по гипотезе энергии формоизменения
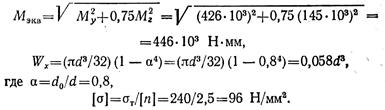
Требуемый наружный диаметр вала
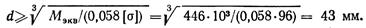
Принимаем d = 45 мм, тогда d0 = 0,8 * 45=36 мм.
Пример 4. Проверить прочность промежуточного вала (рис. 2.71) цилиндрического прямозубого редуктора, если вал передает мощность N = 12,2 кВт при частоте вращения п = 355 об/мин. Вал изготовлен из стали Ст5 с пределом текучести σт = 280 Н/мм2. Требуемый коэффициент запаса [n] = 4. При расчете применить гипотезу наибольших касательных напряжений.

Указание. Окружные усилия Р1 и Р2 лежат в горизонтальной плоскости и направлены по касательным к окружностям зубчатых колес. Радиальные усилия T1 и Т2 лежат в вертикальной плоскости и выражаются через соответствующее окружное усилие следующим образом: T = 0,364Р.
Решение
На рис. 2.71, а представлен схематический чертеж вала; на рис. 2.71, б показана схема вала и усилия, возникающие в зубчатом зацеплении.
Определим момент, передаваемый валом:
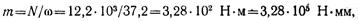
где
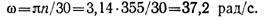
Очевидно, m = m1 = m2 (скручивающие моменты, приложенные к валу, при равномерном вращении равны по величине и противоположны по направлению).
Определим усилия, действующие на зубчатые колеса.
Окружные усилия:
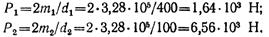
Радиальные усилия:

Рассмотрим равновесие вала АВ, предварительно приведя силы Р1 и Р2 к точкам, лежащим на оси вала.
Перенося силу Р1 параллельно самой себе в точку L, надо добавить пару сил с моментом, равным моменту силы Р1 относительно точки L, т. е.
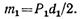
Эта пара сил (момент) условно показана на рис. 2.71, в в виде дугообразной линии со стрелкой. Аналогично при переносе силы Р2 в точку К надо присоединить (добавить) пару сил с моментом
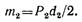
Опоры вала, изображенного на рис. 2.71, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей х и у (выбранная система координат показана на рис, 2.71, б).
Пользуясь расчетной схемой, изображенной на рис. 2.71, г, составим уравнения равновесия вала в вертикальной плоскости:
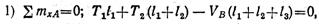
откуда
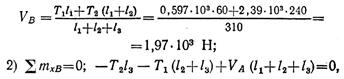
откуда
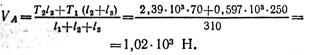
Составим проверочное уравнение:
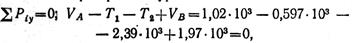
следовательно, опорные реакции в вертикальной плоскости определены верно.
Рассмотрим равновесие вала в горизонтальной плоскости:
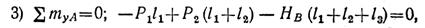
откуда

откуда
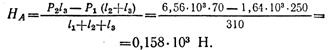
Составим проверочное уравнение:
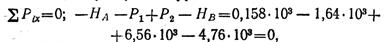
следовательно, опорные реакции в горизонтальной плоскости определены верно.
Эпюры крутящих моментов Мz и изгибающих моментов Мх и Му представлены на рис. 2.71, д.
Опасным является сечение К (см. рис. 2.71, г, д). Эквивалентный момент по гипотезе наибольших касательных напряжений
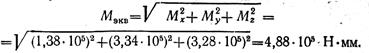
Эквивалентное напряжение по гипотезе наибольших касательных напряжений для опасной точки вала
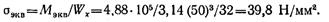
Коэффициент запаса
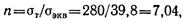
что значительно больше [n] = 4, следовательно, прочность вала обеспечена.
При расчете вала на прочность не учтено изменение напряжений во времени, поэтому и получился такой значительный коэффициент запаса.
Пример 5. Определить размеры поперечного сечения бруса (рис. 2.72, а). Материал бруса — сталь 30XГС с условными пределами текучести при растяжении и сжатии σо ,2р = σтр = 850 Н/мм2, σ0,2c = σTc = 965 Н/мм2. Коэффициент запаса [n] = 1,6.

Решение
Брус работает на совместное действие растяжения (сжатия) и кручения. При таком нагружении в поперечных сечениях возникают два внутренних силовых фактора: продольная сила и крутящий момент.
Эпюры продольных сил N и крутящих моментов Mz показаны на рис. 2.72, б, в. В данном случае определить положение опасного сечения по эпюрам N и Mz невозможно, так как размеры поперечных сечений участков бруса различны. Для выяснения положения опасного сечения следует построить эпюры нормальных и максимальных касательных напряжений по длине бруса.
По формуле
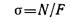
вычисляем нормальные напряжения в поперечных сечениях бруса и строим эпюру о (рис. 2.72, г).
По формуле

вычисляем максимальные касательные напряжения в поперечных сечениях бруса и строим эпюру ттах (рис* 2.72, д).
Вероятно, опасными являются точки контура поперечных сечений участков АВ и CD (см. рис. 2.72, а).
На рис. 2.72, e показаны эпюры σ и τ для поперечных сечений участка АВ.
Напомним, в данном случае (брус круглого поперечного сечения работает на совместное действие растяжения — сжатия и кручения) равноопасными являются все точки контура поперечного сечения.
На рис. 2.72, ж показаны напряжения на исходных площадках в опасной точке.
 |
Главные напряжения в опасной точке участка АВ:
По гипотезе прочности Мора эквивалентное напряжение для опасной точки этого участка
 |
На рис. 2.72, з показаны эпюры а и т для поперечных сечений участка CD.
На рис. 2.72, и показаны напряжения на исходных площадках в опасной точке.
Главные напряжения в опасной точке участка CD: 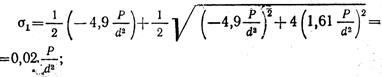
 |
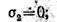
По гипотезе прочности Мора эквивалентное напряжение для опасной точки рассматриваемого участка

Опасными оказались точки контура поперечных сечений участка АВ.
Условие прочности имеет вид:

откуда
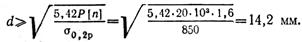
Пример 2.76. Определить допускаемое значение силы Р из условия прочности стержня ВС (рис.2.73).Материал стержня — чугун с пределом прочности при растяжении σвр = 150 Н/мм2 и пределом прочности при сжатии σвс = 450 Н/мм2. Требуемый коэффициент запаса [n] = 5.
 Указание. Ломаный брус АBС расположен в горизонтальной плоскости, причем стержень AВ перпендикулярен к ВС. Силы Р, 2Р, 8Р лежат в вертикальной плоскости; силы 0,5 Р, 1,6 Р — в горизонтальной и перпендикулярны стержню ВС; силы 10Р, 16Р совпада ют с осью стержня ВС; пара сил с моментом m = 25Pd расположена в вертикальной плоскости, перпендикулярной оси стержня ВС.
Указание. Ломаный брус АBС расположен в горизонтальной плоскости, причем стержень AВ перпендикулярен к ВС. Силы Р, 2Р, 8Р лежат в вертикальной плоскости; силы 0,5 Р, 1,6 Р — в горизонтальной и перпендикулярны стержню ВС; силы 10Р, 16Р совпада ют с осью стержня ВС; пара сил с моментом m = 25Pd расположена в вертикальной плоскости, перпендикулярной оси стержня ВС.
Решение
Приведем силы Р и 0,5Р к центру тяжести поперечного сечения В.
Перенося силу Р параллельно самой себе в точку В, надо добавить пару сил с моментом, равным моменту силы Р относительно точки В, т. е. пару с моментом m1 = 10 Pd.
Силу 0,5Р переносим вдоль ее линии действия в точку В.
Нагрузки, действующие на стержень ВС, показаны на рис. 2.74, а.
Строим эпюры внутренних силовых факторов для стержня ВС. При указанном нагружении стержня в его поперечных сечениях их возникает шесть: продольная сила N, поперечные силы Qx и Qy, крутящий момент Mz изгибающие моменты Мх и Му.
Эпюры N, Мz, Мх, Му представлены на рис. 2.74, б (ординаты эпюр выражены через Р и d).
Эпюры Qy и Qx не строим, так как касательные напряжения, соответствующие поперечным силам, имеют малую величину.
В рассматриваемом примере положение опасного сечения не очевидно, Предположительно, опасны сечения К (конец участка I) и С.
 |
Определим величину и плоскость действия изгибающего момента Ми в сечении К, изображённом отдельно на рис. 2.74, в. На этом же рисунке показаны эпюры σИ, σN, τ для сечения К.
Опасной является точка L. Напряжения на исходных площадках в точке L (рис. 2.74, г):

 |
Главные напряжения в точке L:
По гипотезе прочности Мора эквивалентное напряжение для точки L

Определим величину и плоскость действия изгибающего момента Ми в сечении С, изображенном отдельно на рис. 2.74, д. На этом же рисунке показаны эпюры σИ, σN, τ для сечения С.
Напряжения на исходных площадках в точке Н (рис. 2.74, е)
 |
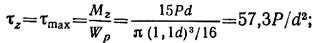
Главные напряжения в точке Н:
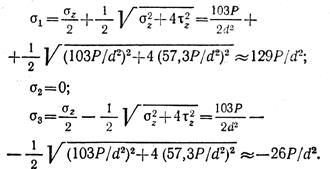
По гипотезе прочности Мора эквивалентное напряжение для точки Н
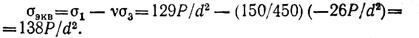
Напряжения на исходных площадках в точке Е (рис. 2.74, ж):
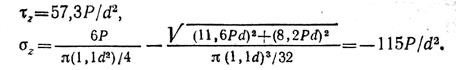
Главные напряжения в точке Е:
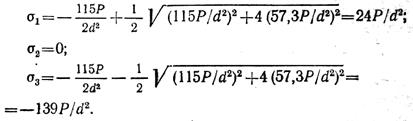
По гипотезе прочности Мора эквивалентное напряжение для точки Е
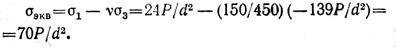
Опасной оказалась точка L, для которой
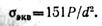
Условие прочности имеет вид:

откуда

Контрольные вопросы и задания
1. Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения?
2. Напишите условие прочности для расчета вала.
3. Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипотезе энергии формоизменения.
4. Как выбирается опасное сечение при расчете вала?
Дата добавления: 2020-08-31; просмотров: 600;











