Початкові відомості про хвилі

Хвилею називають процес розповсюдження в просторі коливань частинок середовища. Самі частки не переміщаються в просторі обсягу середовища, а рухаються біля своїх положень рівноваги.

Залежно від того, напрямки коливань частинок середовища збігаються або перпендикулярні напрямку розповсюдження хвилі, розрізняють хвилі поздовжні і поперечні.

Фронтом хвилі називають геометричне місце точок, до яких у процесі поширення хвилі коливання доходять в один і той же момент часу. Хвильовий фронт відокремлює область простору, де частки середовища знаходяться в збуреному стані, від області, де коливання ще не виникли.

Хвильовою поверхнею називають поверхню, яка проходить через положення рівноваги частинок, що коливаються в однаковій фазі.

Хвилі називають плоскими, сферичними або циліндричними, якщо їх хвильові поверхні являють собою площини, сферичні і циліндричні поверхні відповідно. Напрямки поширення хвилі перпендікулярні хвильовим поверхням.

Нехай якась скалярна фізична величина S (наприклад, зсув частинок середовища) залежить тільки від однієї просторової координати x і часу t, тобто 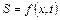. Легко бачити, що, якщо структура аргументу функції 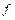має вигляд 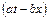, то значення функції 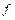, яке вона мала в точках площини 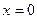в момент часу t, буде тим же в точках площини 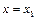, але із запізненням за часом на 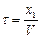, де .

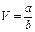Дійсно, це підтверджується порівнянням між собою виразів:

,

.

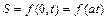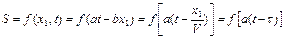У такому випадку говорять, що обурення фізичної величини S поширюється у позитивному напрямку осі x зі швидкістю .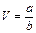

Будь-яка функція від аргументу виду 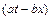висловлює обурення поширення уздовж осі х. Якщо графік залежності S від x має піднесення і западини та їх розташування різному в різні моменти часу, то процес, що описується рівнянням, 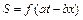називають плоскою хвилею.

Хвиля, що поширюється в негативному напрямі осі x, описується рівнянням

.

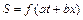Гармонійні хвилі

Хвилі, що описуються гармонійної функцією, називаються гармонійними хвилями. Рівняння плоскої гармонійної хвилі, що розповсюджується в позитивному напрямі осі x, прийнято записувати у вигляді:

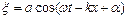. (8.1)

Введемо визначення: величину 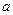називають амплітудою хвилі, 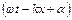- фаза хвилі, 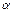- початкова фаза; вона визначається вибором початку відліку координати x і часу t. Величина 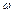є циклічна (кругова) частота коливань частинок середовища. З періодичності функції 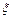за часом знаходимо 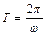- період коливань частинок.

Коефіциєнт 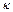називають хвильовим числом. Його можна представити як ,

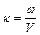де v – швидкість поширення хвилі.

Відстань, на яку поширюється хвиля за час, що дорівнює періоду коливань частинок, називається довжиною хвилі :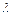

.

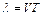Довжина хвилі пов'язана з хвильовим числом, співвідношенням:

.

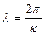Фазовою швидкістю хвилі називається швидкість переміщення в просторі поверхні постійної фази хвилі. З умови сталості фази для гармонійної плоскої хвилі (8.1) маємо:

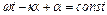. (8.2)

Це рівняння є рівнянням площини у просторі. Швидкість її переміщення і є фазовою швидкістю хвилі:

.

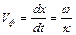Зазначимо, що у разі гармонійної хвилі фазова швидкість 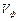збігається зі швидкістю хвилі, тобто зі швидкістю поширення коливань частинок середовища.

Хвильовим вектором 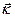називають вектор, який визначається виразом:

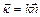
або

,

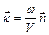де 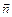- одиничний вектор, перпендикулярний до хвильової поверхні.