ЕЛЕКТРОМАГНІТНІ ХВИЛІ


 

Струм зміщення

 

Повернемося ще раз до причини виникнення магнітного поля. Ми говорили про те, що причиною виник­нення магнетизму є рух електричних зарядів. А що ж відбувається у випадку розімкненого електричного кола, коли відсутній сам провідник (наявність конденсатора оз­начає по суті розрив кола)? Як пояснити наявність змінного струму в такому колі?

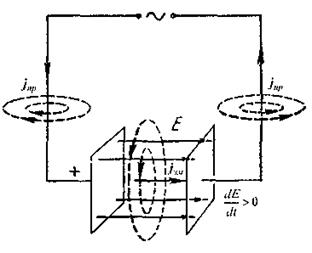
Мал. 2.39.

Фізичне пояснення дав видатний фізик Джеймс Кларк Максвелл (1831-1879 рр). Це пояснення базується на по­нятті струмів зміщення, які є свого роду продовженням звичних струмів провідності. Максвелл припустив, що маг­нітне поле може збуджуватись не тільки електричним струмом, а й змінним електричним полем.

Знайдемо вираз для сили струму зміщення. Для цього розглянемо проходження змінного струму по колу, в яке увімкнений конденсатор (мал. 2.39). Конденсатор не пе­решкоджає протіканню змінного струму і можна вважати, що звичайний струм провідності 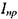замикається в конден­саторі струмом зміщення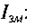

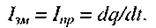
Заряд на обкладках плоского конденсатора

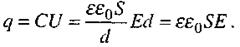
Тоді сила струму зміщення в конденсаторі

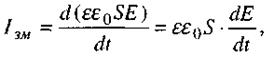
а густина струму зміщення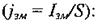

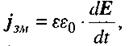(2.81)

або, враховуючи зв'язок між векторами напруженності Е й індукції електричного поля (2.3),

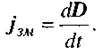(2.82)

Отже, густина струму зміщення дорівнює швидкості зміни з часом індукції електричного поля. Із (2.81) випли­ває, що вектор 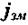направлений в той самий бік, що й 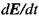Тобто, якщо конденсатор заряджається 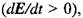то вектори 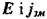мають однаковий напрям, якщо ж 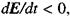то

вектори 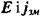протилежні за напрямом.

Пригадаємо, що у діелектрику вектор індукції елек­тричного поля пов'язаний з векторами напруженості і 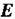і по­ляризації Р співвідношенням

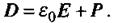
Тоді густина струму зміщення в діелектрику складаєть­ся з двох доданків:

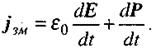(2.83)

Перший доданок має місце і у вакуумі, другий доданок характеризує зміщення електричних зарядів у діелектрику, яке й зумовлює нагрівання діелектрика.

Найголовніша властивість струму зміщення полягає в тому, що він, як і струм провідності, створює вихрове маг­нітне поле.

Струм зміщення виникає завжди, коли змінюється з ча­сом електричне поле. Він може бути і в провідниках, і в діелектриках, і в вакуумі. Густина повного струму дорів­нює сумі густин струмів провідності і зміщення:

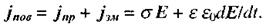(2.84)

Залежно від електропровідності середовища і швид­кості зміни поля (частоти) доданки в рівнянні (2.84) відіграють різну роль. Припустимо, що напруженість поля змінюється за гармонічним законом 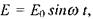тоді густина струму зміщення: 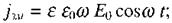густина струму провідності 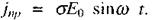Відношення максимальних (амплітудних) значень густини струму провідності та зміщення: 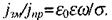Для біологічних тканин 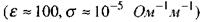при частотах, близьких до 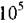Гц, амплітудні значення цих струмів є величинами одного порядку. Із збільшенням частоти електромагнітних коли­вань зростає вклад струму зміщення в повний струм.

Проходження струму зміщення в різних середовищах супроводжується виділенням теплоти, яка може бути розра­хована за законом Джоуля-Ленца (2.41):

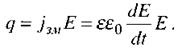(2.85)

Якщо напруженість поля змінюється за гармонічним законом 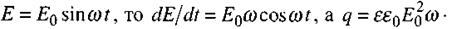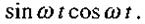Тобто

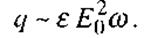(2.86)

У випадку однорідного діелектрика кількість теплоти може бути розрахована за формулою:

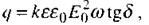(2.87)

де 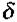- кут між вектором напруженості Е та вектором поля­ризації Р, його називають кутом діелектричних втрат, а 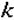-деякий сталий коефіцієнт.

 

Рівняння Максвелла

 

Дж. К. Максвелл записав свої геніальні рівняння в 1865 р. Рівняння Максвелла - це фундаментальні рівняння елек­тродинаміки, які описують електромагнітні явища в будь-якому середовищі. Вони узагальнюють експериментальні і теоретичні праці фізиків першої половини XIX ст. і, насам­перед, дослідження М. Фарадея. Основні закони електроди­наміки Максвелл сформулював у вигляді чотирьох рівнянь, які подамо в інтегральній формі, як в найбільш простій і наочній.

Перше рівняння Максвелла спирається на закон Біо-Савара-Лапласа та поняття струму зміщення. Виділимо в провіднику, в якому існує змінний струм, довільну площад­ку 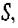обмежену контуром 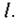Тоді

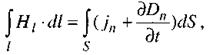(2.88)

де 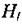- проекція вектора напруженості магнітного поля на напрям дотичної до контура 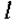у даній точці, 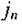- нормальна до вибраної площадки складова густини струму провідності, 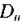- нормальна до площадки складова вектора електричної індукції. Тут вжита частинна похідна dD/dt, щоб врахувати факт залежності D як від часу, так і від про­сторової координати. Струм зміщення виникає лише тоді, коли D змінюється з часом. Це рівняння показує, що магнітне поле вихрове і що воно виникає незалежно від на­явності постійних магнітів. Виникнення магнітного поля зумовлене двома факторами: рухом електричних зарядів (струм провідності) і зміною в часі електричного поля (струм зміщення).

Друге рівняння відображає закон електромагнітної індукції Фарадея:

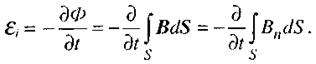
ЕРС, як відомо, дорівнює роботі сторонніх сил по пе­реміщенню одиничного заряду, тобто 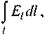тому матимемо

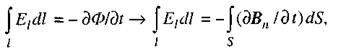(2.89)

де 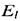— проекція вектора напруженості електричного поля на напрям дотичної до контура у даній точці, 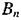- нормальна до поверхні складова вектора магнітної індукції. З цього рівняння видно, що крім електростатичного поля в природі існує електричне поле, джерелом якого є змінне магнітне поле. Всяка зміна електричного поля зумовлює появу змінного магнітного поля, лінії напруженості якого замк­нені і охоплюють лінії електричного поля (перше рівняння); всяка зміна магнітного поля зумовлює появу змінного електричного поля, лінії напруженості якого замкнуті й охоплюють лінії магнітного поля (друге рівняння).

Третє рівняння Максвелла показує, що джерелом електричного поля є електричні заряди:

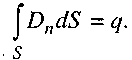
Ліва частина цього рівняння - потік вектора індукції електричного поля через замкнену поверхню площею 5.

Четверте рівняння відображає факт відсутності маг­нітних зарядів. Повний потік вектора магнітної індукції В через замкнену поверхню площею S дорівнює нулю:

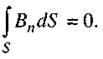
Наведені рівняння Максвелла не враховують будову речовини і взаємодію електромагнітного поля з частинками речовини. Вплив середовища на електромагнітне поле за­дається через його електропровідність, а також діелектрич­ну ε і магнітну 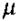проникності. Тому до рівнянь Максвелла слід додати ще три рівняння, які називаються матеріальни­ми:

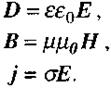
Рівняння Максвелла описують величезне коло явищ (електродинаміка, оптика, електротехніка, радіотехніка, ас­трофізика, фізика плазми тощо). Теорія Максвелла не тільки пояснила вже відомі факти, а й передбачила нові і важливі явища. Абсолютно новим у цій теорії було припу­щення Максвелла про магнітні поля струмів зміщення. На основі цього припущення Максвелл предбачив існування електромагнітних хвиль, тобто змінного електромагнітного поля, яке поширюється в просторі з певною швидкістю. Теоретичне дослідження властивостей електромагнітних хвиль привело згодом Максвелла до створення електро­магнітної теорії світла. Пізніше експериментальне вдалося отримати електромагнітні хвилі і провести досліди, які бли­скуче підтвердили електромагнітну теорію світла, а з нею і всю теорію Максвелла.

 

2.5.3. Плоскі електромагнітні хвилі. Вектор Умова-Пойнтінга

 

Періодичні зміни електричного чи магнітного поля в деякій області простору дають початок сукупності послідовних взаємопов'язаних перетворень цих полів, котрі охоплюють все нові області простору. Обидва ці поля є вихровими, причому вектори Е та Н розміщені у взаємно перпендикулярних площинах. Електромагнітне поле, яке періодично змінюється, поширюючись у просторі, утворює електромагнітну хвилю.

Для ізотропного діелектрика, в якому немає вільних електричних зарядів, з рівнянь Максвелла випливає:

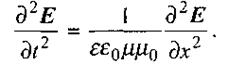(2.90)

Таке ж рівняння можна отримати і для напруженості магнітного поля Н. Рівняння (2.90) свідчить, що напру женість електричного Е (а значить, і магнітного Н) поля за­довольняє хвильовому рівнянню, і швидкість поширення електромагнітних хвиль

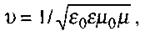(2.91)

де 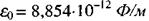- електрична стала, 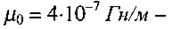магнітна стала, 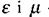- відносні діелектрична та магнітна проникності середовища. У вакуумі швидкість поширення електромагнітних хвиль дорівнює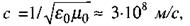

тоді як в середовищі 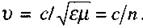. Величину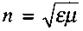

називають абсолютним показником заломлення середо­вища. Він показує, у скільки разів швидкість електромаг­нітної хвилі в середовищі менша, ніж у вакуумі. Розв'язок (2.90) має вигляд плоскої хвилі:

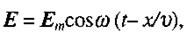(2.92)

або, якби хвильове рівнян­ня було записано для маг­нітної компоненти поля Н, то де Е і Н - миттєві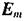, а та 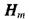- амплітудні значення напруженості електричного та магнітного полів, 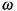-циклічна частота коливань

,де 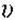- швидкість поширення хвилі.

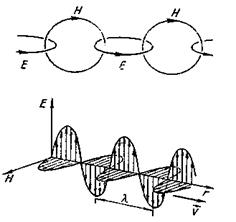
Мал. 2.40.

Вектори Е і Н одночасно досягають максиму­му і одночасно перетворюються в нуль, тобто коливаються в однаковій фазі; вони взаємно перпендикулярні і перпен­дикулярні до вектора швидкості 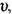тобто електромагнітна хвиля поперечна (мал. 2.40).

Електромагнітна хвиля в напрямку свого поширення переносить певну енергію. Енергія електромагнітного поля в одиниці об'єму (густина енергії електромагнітного поля) дорівнює

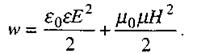(2.93)

Перший доданок - густина енергії електричного поля, другий - магнітного. З рівнянь Максвелла випливає, що в довільний момент часу має місце рівність

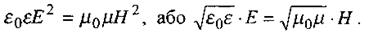(2.94)

Таким чином, в електромагнітній хвилі напруженості електричного і магнітного полів пропорційні одна одній: 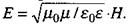Множник перед Я називають хвильовим опором середовища. Для вакууму 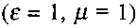хвильовий

опір дорівнює приблизно 377 Ом. Крім того, з (2.94) видно, що електрична і магнітна складові електромагнітного поля рівноправні. Використавши (2.94), вираз для густини енергії (2.93) можна переписати у вигляді:

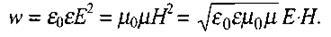(2.95)

Густина потоку енергії електромагнітного поля І дорів­нює добутку густини енергії 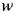і швидкості поширення хвилі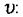

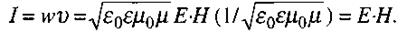(2.96)

Вектор густини потоку енергії електромагнітного поля дорівнює 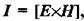напрямок її перенесення збігається з векторним добутком 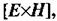а значить, і з швидкістю поширення хвилі, тобто визначається за пра­вилом правого гвинта. Цей вектор носить назву вектора Умова-Пойнтінга.

 


Дата добавления: 2020-11-18; просмотров: 378;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.034 сек.