Поняття про нелінійні коливання

Теорія нелінійних коливань вивчає періодичні коливальні процеси, які відбуваються в системах, рух яких описується нелінійними диференціальними рівняннями. Такі коливальні системи називаються нелінійними.

В більшості випадків, що розглядались раніше, "лінійність" системи є результатом спрощення реальної системи. Наприклад, опір середовища (так зване в'язке тертя) залежить від швидкості і зі зменшенням останньої може бути надзвичайно малим. Залежність сили опору від швидкості має вигляд кривої, що представлена на рис.4.20

Для невеликих швидкостей, наприклад, в межах 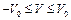, ця крива практично не відрізняється від прямої, тобто заміна ділянки AB кривої прямолінійним відрізком є припустимою, і тому "лінеаризація" такого процесу у вказаних межах зміни швидкості з великим відсотком відповідає реальному процесу.

Для 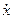<20 м/с маємо лінійну залежність сил опору від швидкості руху тіла вважають лінійною 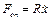, тобто рівняння руху має вигляд .

При зростанні швидкості 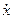>20 м/с спостерігаємо нелінійну залежність , де , а рівняння набуває вигляду .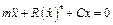

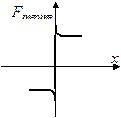
рис.4.21

Інша справа – сухе (кулонівське) тертя, спрощена характеристика якого представлена на рис.4.21

Лінеаризація рівняння з сухим тертям неможлива, яким би малим не був проміжок, на якому розглядається зміна швидкості біля початку координат. Крім цього, існує ряд матеріалів, які не відповідають закону Гука навіть при малих деформаціях. Залежність сили від деформації таких матеріалів зображена на рис.4.22

рис.4.22

Матеріали, що відповідають залежності 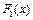відносяться до матеріалів з "жорсткою" характеристикою, а - "м'якою".

Можна навести ще багато прикладів, де лінійна трактовка задачі про коливання не дає можливості отримати результати, що відповідають, наприклад, експериментальним.

Назвемо деякі відмінні особливості нелінійних коливань від лінійних.

1. Через нелінійність коливальної системи порушується принцип суперпозиції, тобто, наприклад, сума двох коливальних рухів може бути не коливальним рухом. Якщо сила, що діє на систему, розкладена в ряд Фур'є, то дія її на нелінійну систему не буде дорівнювати лінійній сумі дій кожної окремої гармонічної складової цього ряду.

2. Вільні коливання реальних лінійних систем завжди затухаючі. Періодичні коливання в лінійних системах можливі тільки в формі так званих вимушених коливань, що виникають внаслідок дії зовнішніх періодичних збурюючих сил.

В нелінійних системах і при наявності сил опору можливі стійкі періодичні вільні коливання. Втрата енергії в деяких нелінійних системах може бути автоматично скомпенсована за рахунок отримання її із неколивального джерела. Це має місце в так званих автоколивальних системах, прикладом якої є годинник з маятником.

3. В лінійних системах вимушені коливання від гармонічної збурюючої силою відбуваються з частотою або періодом останньої.

В нелінійних системах вимушені коливання від збурюючої сили можуть відбуватися не тільки з періодом збурюючої сили, а й з періодом кратним даному, тобто, наприклад, в нелінійній системі з одним ступенем вільності, коли діє тільки одна гармонічна збурююча сила, можливі декілька резонансних режимів.

4. В лінійних системах власні частоти не залежать від початкоих умов, і, власне, від амплітуди. Змінити частоту власних коливань лінійної системи можна тільки шляхом суттєвих змін конструкції системи, розподілу в ній мас та пружностей.

В нелінійних системах власна частота, частіше за все, залежить від амплітуди коливань.

Для опису поведінки нелінійних систем розроблено безліч геометричних, аналітичних та чисельних методів. Найбільшого розвитку набули так звані методи малого параметра, коли нелінійність системи є малою і розв'язання відповідних диференціальних рівнянь будується за допомогою розкладання їх в ряди за степенями малого параметра.

Основоположником класичного методу розкладання шуканого розв'язку за степенями малого параметра є Анрі Пуанкаре.

Метод Пуанкаре відноситься до коливальних систем, в рівняння руху яких входить малий параметр μ і система має періодичний розв'язок, коли цей параметр дорівнює нулю. Такі системи називають системами Пуанкаре. Частинним випадком систем Пуанкаре являються так звані квазілінійні системи, в яких нелінійні члени входять множниками при малому параметрі μ і ці системи обертаються при μ=0 в лінійні рівняння зі сталими коефіцієнтами. Загальний вигляд диференціального рівняння, що описує квазілінійну систему:

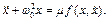
Основна ідея метода Пуанкаре заключається в тому, що можливі в квазілінійних системах при досить малому μ періодичні рухи розташовані поблизу періодичних рухів відповідних лінійних систем, в які перетворюються нелінійні системи при μ=0. Періодичні розв'язки лінійної системи, поблизу яких виникають періодичні розв'язки квазілінійної системи, називаються по відношенню до нелінійної породжуючими. В залежності від типу квазілінійної системи такі породжуючі системи бувають двох видів.

Перший відноситься до випадку, коли породжуюча система (породжуючі диференціальні рівняння) задаються диференціальними рівняннями вимушених коливань з періодичною правою частиною, яка залежить від часу (не автономна система). Цей породжуючий розв'язок є єдиним періодичним розв'язком, породжуючої системи, поблизу якого розташований єдиний періодичний розв'язок квазілінійної системи. Така схема розв'язку має місце для квазілінійної системи, що відповідає рівнянню:

.

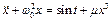Другий випадок знаходження породжуючих систем буде мати місце для автономної квазілінійної системи

.

Породжуюче рівняння

має розв'язок 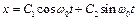, що залежить від довільних параметрів С₁ і С₂. В цьому випадку квазілінійна система може мати декілька періодичних розв'язків, які виникають поблизу деяких відібраних розв'язків породжуючої системи з певними значеннями параметрів С₁ і С₂.

Незважаючи на тип квазілінійної системи (автономна чи неавтономна) Пуанкаре запропонував будувати розв'язок нелінійних рівнянь у вигляді ряду за степенями малого параметру μ. Тобто

Цей метод розв'язання нелінійних рівнянь удосконалив О.М.Крилов. Суть його методу полягає у сумісному і одночасному розкладанні за степенями малого параметра μ шуканої функції x(t) і квадрата шуканої частоти, так як в нелінійних системах резонансна частота залежить від вхідної величини (наприклад, від величини деформації матеріалу).