Кінематичне збурення

При кінематичному збуренні коливань задача полягає в тому, щоб амплітуда абсолютного коливання тіла (x_k) була б якомога меншою.

Для цього випадку рівняння Лагранжа другого роду записується як:

;

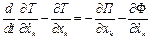x_k – абсолютна координата руху.

Запишемо вирази для кінетичної та потенціальної енергій і функції Релея:

; ; .

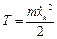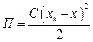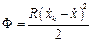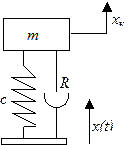
рис. 4.14

Знайдемо похідні:

; ;

.

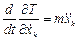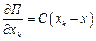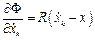Звідси отримаємо рівняння:

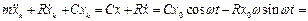
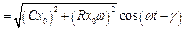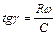, , або

.

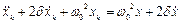Введемо оператор диференціювання:

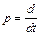. Тоді,

.

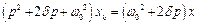Звідси маємо: .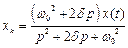

Отже, з точки зору математики, кінематичне та силове збурення є анологічними.

Введемо поняття коефіцієнта динамічності системи ( ).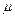

.

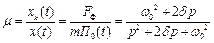При гармонічному сигналі 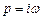, отже

; .

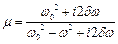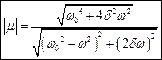Якщо 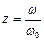; 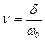, тоді ;

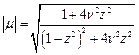рис. 4.15

Очевидно, що ефективною умовою віброзахисту і віброізоляції є 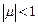, або ;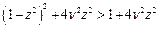

;

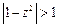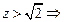
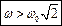- умова ефективного виконання віброізоляції та вібро-захисту.

Отже, для того, щоб розв'язати задачу віброізоляції або віброзахисту, незалежно від того, яке збурення коливань є (силове чи кінематичне), параметри системи мають бути вибрані так, щоб частота власних коливань була набагато меншою за частоту збурення. Дія вібрації на тіло або фундамент зменшиться, якщо частота ω вібрації більше в 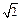разів частоти ω₀ вільних коливань тіла.

Причому, якщо 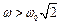, то чим менше демпфірування в системі, тим ефект віброзахисту або віброізоляції більший (рис.4.15).