Прямые методы формирования весовых коэффициентов. Алгоритмы непосредственного обращения матриц.

После усреднения выражения (16.3), полагая, что весовые коэффициенты меняются значительно медленнее, чем входные сигналы, можно получить следующее дифференциальное уравнение для весовых коэффициентов:

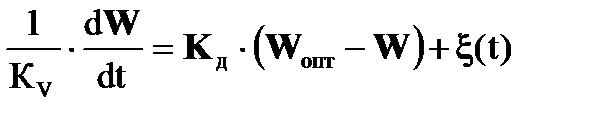, (16.5)

где 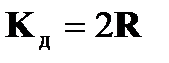- матрица крутизн многомерного дискриминатора весовых коэффициентов;

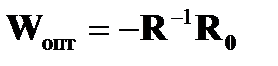- оптимальное значение вектора весовых коэффициентов, минимизирующее мощность помехи и соответствующее нулевым средним значениям сигналов ошибок;

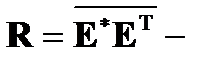корреляционная матрица сигналов, принятых компенсационными каналами;

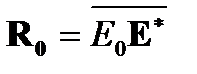- вектор корреляции сигналов, принятых основным и компенсационными каналами;

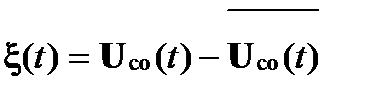- вектор случайных составляющих сигнала ошибки.

Таким образом, адаптивное устройство градиентного вида может быть представлено многомерной линейной следящей системой, матрица крутизн которой 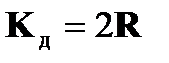с точностью до скалярного множителя определяется корреляционной матрицей сигналов на входе.

Оптимальное значение весового вектора 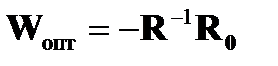, минимизирующее мощность помехи на выходе, определяется через корреляционную матрицу сигналов помехи 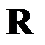и вектор корреляции .

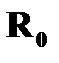Следовательно, требуемый весовой вектор можно вычислить непосредственно в соответствии с выражением:

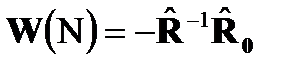, (16.6)

где: 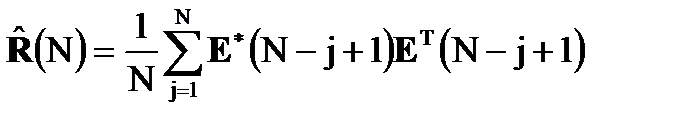- максимально правдоподобная оценка корреляционной матрицы помех;

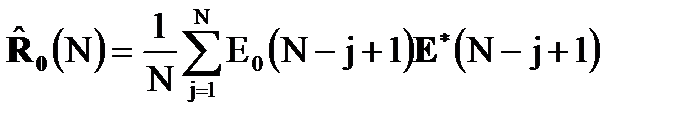- максимально правдоподобная оценка вектора корреляции помех;

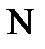- объем обучающей выборки.

Алгоритм (16.6) называется алгоритмом непосредственного обращения матрицы (SMI), который в отличие от градиентного алгоритма обеспечивает гарантированное окончание переходных процессов.

Вычислительная сложность алгоритма НОМ составляет порядка N³ операций умножения на каждой итерации.

Обращение матрицы выполняют одним из трех методов вычислительной математики:

- методом Хаусхолдера;

- методом Гивенса;

- модифицированным методом Грамма-Шмидта.

Метод Хаусхолдера характеризуется меньшим количеством перемножителей, однако неприспособлен к параллельным вычислениям. Поэтому предпочтителен при применении микропроцессоров, а не при аппаратной реализации.

Метод Гивенса характеризуется высокой степенью распараллеливания операций, поэтому рекомендуется для аппаратной реализации.

Модифицированный метод Грамма-Шмидта подобен методу Хаусхолдера, но менее чувствителен к ошибкам округления.