Собственный шум цифрового фильтра

Собственный шум цифрового фильтра – это шум, обусловленный квантованием результатов умножения.

В состав цифрового фильтра входят умножители, каждый из которых является источником шума. Произведение двух b-разрядных чисел имеет удвоенную разрядность 2b. Для использования результата произведения в последующих вычислениях, его ограничивают исходными b разрядами. Это приводит к ошибке округления, дисперсия которой определяется выражением:

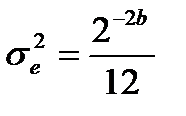. (15.4)

Оценка параметров собственного шума осуществляется в три этапа:

1) Составляется линейная модель цифрового фильтра, учитывающая шумы квантования в точках перемножения;

2) Определяется реакция цифрового фильтра на каждый шумовой сигнал;

3) Вычисляется результирующий собственный шум на выходе системы и его характеристики.

При составлении линейной модели каждый умножитель заменяется последовательным соединением идеального умножителя (с неограниченным количеством разрядов) и сумматора, на второй вход которого поступает ошибка квантования :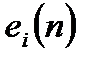

.

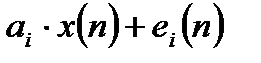Реакция цифрового фильтра на каждый шумовой сигнал получается в соответствии с выражением:

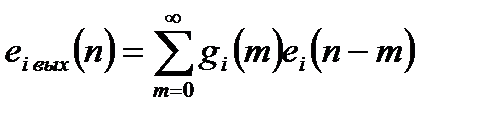, (15.5)

где 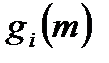- импульсная характеристика части цифрового фильтра от точки приложения 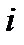-ого источника шума до выхода системы.

Дисперсия составляющей выходного шума определяется выражением:

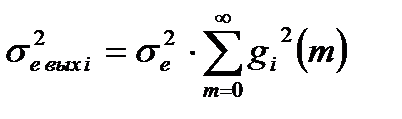. (15.6)

Суммарная дисперсия выходного шума цифрового фильтра записывается следующим образом:

, (15.7)

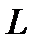- количество перемножителей.

Линейная модель цифрового рекурсивного фильтра первого порядка с указанием шумов квантования приведена на рисунке 15.1.

Рисунок 15.1 – линейная модель рекурсивного фильтра 1-го порядка для анализа эффектов квантования

Пусть передаточная функция цифрового полосового фильтра имеет вид:

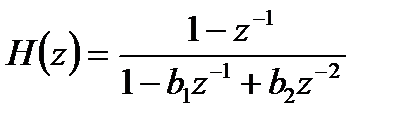. (15.8)

Для этого случая шумы квантования и собственный шум фильтра описываются выражениями, приведенными в Таблице 15.1.

Таблица 15.1. Дисперсия шума на выходе полосового фильтра для различных структурных реализаций ЛДС

	Прямая форма, каноническая форма 2	Обращенная форма, каноническая форма 1
Шум квантования
Собственный шум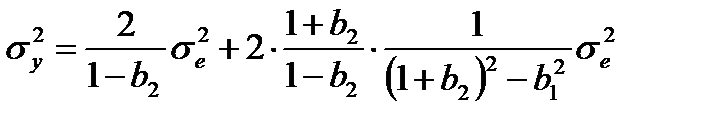

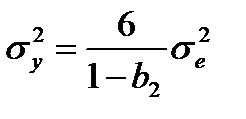
Из Таблицы 15.1 следует, что дисперсии шумов квантования равны для всех рассмотренных структурных реализаций.

Дисперсия внутреннего шума для прямой формы и канонической формы 2 меньше дисперсии внутреннего шума обращенной формы и канонической формы 1.

Следует отметить, что каскадная и параллельная структуры обладают наилучшими шумовыми свойствами по сравнению с прямой или канонической формами реализации цифровых фильтров высокого порядка.

Литература

Петровский А.А. Методы и микропроцессорные средства обработки широкополосных и быстропротекающих процессов в реальном времени / Под ред. Г.В. Римского. – Мн.: Наука и техника, 1988. – 272 с.

Глинченко А.С. Цифровая обработка сигналов: в 2 ч. Ч.1. Красноярск: Изд-во КГТУ. 2001. 199 с. (п. 4.5)

Основы цифровой обработки сигналов: учебное пособие / Ю.А. Брюханов, А.А. Приоров, В.И. Джиган, В.В. Хрящев; Яросл. гос. ун-т им. П.Г. Демидова. - Ярославль: ЯрГУ, 2013. – 344 с. (с. 155)

Карташов В.Г. Основы теории дискретных сигналов и цифровых фильтров. – М.: Высш. школа, 1982. – 109. (с. 89: показывает, что для рекурсивного фильтра 1-ого порядка при переходе от прямой реализации структурной схемы к канонической дисперсия собственных шумов может снизиться в 10 раз).

Гадзиковский В.И. Цифровая обработка сигналов. М.: СОЛОН-ПРЕСС, 2013. – 766 с. (с. 330: утверждается, что при прямой реализации коэффициенты числителя не влияют на собственные шумы в отличие от канонической реализации, причем для фильтра 3-его порядка дисперсия шумов может отличаться в 100 раз).

Рясный Ю.В., Тихобаев В.Г., Панарин В.И. Математические основы цифровой обработки сигналов. Часть 2. Цифровые фильтры и методы их проектирования: Учебное пособие / СибГУТИ. – Новосибирск, 2009. – 243 с.