Рівняння Максвелла та їх фізичний зміст
Теорія Максвелла стверджує, що між основними величинами, що характеризують електромагнітне поле в довільній точці рухомий або порожнечі, існують прості та універсальні зв'язки, виражені рівняннями:
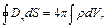 (9.1)
(9.1)
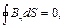 (9.2)
(9.2)
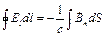 , (9.3)
, (9.3)
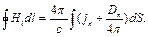 (9.4)
(9.4)
Тут 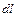
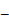 елемент довжини,
елемент довжини, 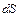
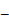 елемент поверхні,
елемент поверхні, 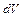
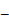 елемент об’єма. Індекс «
елемент об’єма. Індекс « 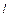 »означає проекцію на напрям елемента
»означає проекцію на напрям елемента 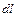 , індекс «
, індекс « 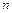 »
» 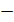 проекцію на напрям нормалі до елемента
проекцію на напрям нормалі до елемента 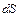 . Інтеграли в лівій частині рівнянь (9.1), (9.4) беруться вздовж замкнутого контуру або по замкненій поверхні.
. Інтеграли в лівій частині рівнянь (9.1), (9.4) беруться вздовж замкнутого контуру або по замкненій поверхні.
Вектор 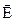
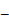 напруженість електричного поля, вектор
напруженість електричного поля, вектор 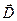
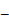 електрична індукція,
електрична індукція, 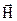 – напруженість магнітного поля, вектор
– напруженість магнітного поля, вектор 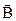
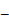 магнітна індукція,
магнітна індукція, 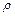 – об'ємна щільність електричного заряду,
– об'ємна щільність електричного заряду, 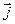 – об'ємна щільність електричного струму,
– об'ємна щільність електричного струму, 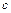 – електродинамічна постійна.
– електродинамічна постійна.
Рівняння (9.1) є вираз теореми Гаусса, згідно з якою потік електричної індукції через замкнену поверхню дорівнює числу 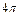 , помноженому на повний електричний заряд, що знаходиться всередині цієї поверхні.
, помноженому на повний електричний заряд, що знаходиться всередині цієї поверхні.
Рівняння (9.2) виражає той факт, що не існує магнітних зарядів; потік магнітної індукції через будь-яку замкнену поверхню дорівнює нулю.
Рівняння (9.3) виражає закон індукції Фарадея: циркуляція електричного поля по довільній замкненій кривій дорівнює зміні потоку магнітної індукції через довільну поверхню, обмежену цією кривою. Знак (-) - це характеристика «лівого» гвинта електричного поля.
Рівняння (9.4) стверджує, що поряд зі струмом провідності 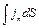 у створенні магнітного поля бере участь величина (так званий раніше - «струм зміщення»)
у створенні магнітного поля бере участь величина (так званий раніше - «струм зміщення») 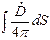 . Це твердження грає в теорії Максвелла фундаментальну роль.
. Це твердження грає в теорії Максвелла фундаментальну роль.
Рівняння (9.1) - (9.4) не вичерпують змісту теорії Максвелла. Подібно до того як для теоретичних досліджень пружних хвиль необхідно, крім законів механіки, знати який в розглянутому середовищі зв'язок між напругою 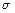 і деформацією
і деформацією 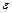 , в електромагнітних явищах необхідно знати зв'язок між
, в електромагнітних явищах необхідно знати зв'язок між 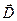 і
і 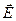 ,
, 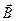 і
і 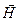 ,
, 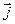 і
і 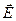 .
.
Середа називається лінійною, якщо компоненти цих векторів пов'язані лінійними співвідношеннями. Більше того, середовища, властивості яких у всіх напрямках однакові, називаються ізотропними. Співвідношення, що розглядаються між векторами в цьому випадку, особливо прості.
Будемо враховувати, що в діелектриках 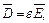
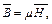
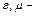 діелектрична і магнітна проникненість (постійні величини), а в металах
діелектрична і магнітна проникненість (постійні величини), а в металах 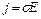 .
.
Дата добавления: 2020-08-31; просмотров: 616;











