Перенесення енергії пружною хвилею. Енергетичні співвідношення

У процесі поширення хвиля переносить енергію з областей простору, залучених у цей процес, в області, де коливання ще не виникли. Процес перенесення енергії характеризують поняттями: потік енергії, вектор щільності потоку енергії, інтенсивність хвилі.

Кількість енергії, що переноситься хвилею через деяку поверхню 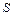за одиницю часу, називають потоком енергії :

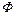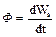, (8.18)

де 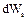– переносима енергія через дану поверхню за час .

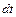Так як потік енергії в різних точках поверхні S може мати різну інтенсивність, то вводиться поняття щільності потоку енергії.

Вектор щільності потоку енергії 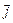визначається як:

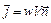, (8.19)

де 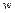– об'ємна щільність хвилі, 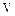– швидкість поширення хвилі, 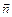– одиничний вектор у напрямку поширення хвилі.

Зв'язок між вектором 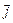і потоком 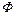встановлюється з таких міркувань: за проміжок часу 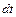хвиля поширюється на відстань 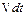; енергія 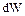, перенесена хвилею, укладена в обсязі похилого циліндра (рис. 8.3; тут 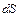довільно орієнтована елементарна площадка) дорівнює

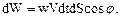(8.20)

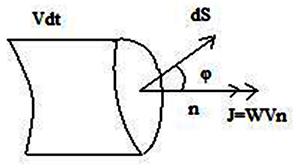
Рисунок 8.3 – Елементарний об'єм з довільно орієнтованою площею і напрямком поширення хвилі.

Запишемо (8.20) у вигляді:

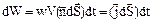. (8.21)

Враховуючи (8.21), потік енергії (8.18) стане рівним:

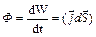. (8.22)

Якщо 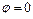, то рівність (8.22) дає зв'язок 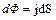, де 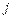– модуль вектора потоку енергії; або

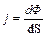. (8.23)

З (8.3) випливає, що модуль вектора щільності потоку енергії дорівнює потоку енергії, яку переносять хвилею через одиничну площадку, перпендикулярну напрямку поширення хвилі.

Ще однією характеристикою хвильового процесу є інтенсивність хвилі. Інтенсивністю хвилі називають величину, рівну модулю середнього за часом вектора щільності потоку енергії:

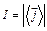. (8.24)

Враховуючи (8.19), можна отримати інше вираження для інтенсивності хвилі:

.

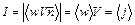Стояча хвиля

Нехай скалярна фізична величина S змінюється за законом:

,

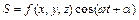тобто величина S у всіх точках простору здійснює гармонічні коливання з однаковою частотою і фазою, але з амплітудами різними для різних точок. Таке явище називають стоячеюй хвилею.

Розглянемо окремий випадок плоскої стоячої хвилі виду 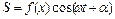. Покажемо, що суперпозиція двох хвиль однакової частоти і амплітуди, що біжать в протилежних напрямках, хвиль утворює стоячу хвилю.

Нехай 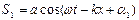і .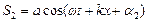
Тоді 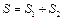перетвориться до виду:

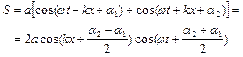. (8.25)

Вираз (8.25) є рівняння стоячої хвилі. Змінюючи початок відліку координати 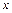і моменту часу 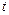рівняння (8.25) можна привести до стандартного виду:

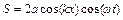. (8.26)

З (8.26) видно, що амплітуда результуючої стоячої хвилі для заданих 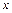в два рази більше амплітуд кожної бігучої хвилі. Максимальні значення амплітуди знаходяться з умови: 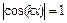. Тоді положення точок простору, де виконується ця умова, визначається рівністю:

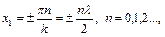(8.27)

де 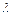– довжина хвилі.

Такі точки називають пучностями стоячої хвилі. Точки простору, в яких коливання величини 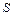відсутні, називають вузлами стоячої хвилі.