КИНЕТИКА ЗАМЕДЛЕНИЯ НЕЙТРОНОВ

С разработкой компактных нестационарных источников — импульсных и модулированных генераторов нейтронов с большим выходом нестационарные нейтронные поля стали «инструментом» исследования состава и свойств вещества не только в ядерной геофизике, но и во многих других областях науки и техники. Возможности использования наносекундной измерительной аппаратуры, потребности спектрометрии нейтронов по времени замедления (а также измерение реактивности и других критических параметров реакторных систем, проблема получения холодных нейтронов) — все это сделало энергетически-временное распределение нейтронов в веществе объектом интенсивного экспериментального и теоретического изучения [30].

С использованием генераторов нейтронов реализованы, в частности, импульсный метод количественного определения урана в горных породах, основанный на измерении временного распределения мгновенных нейтронов деления в надтепловой части спектра, а также спектрально-резонансный анализ горных пород по времени замедления нейтронов. Для интерпретации результатов измерений с импульсным генератором необходимо знать физические закономерности кинетики замедления нейтронов.

Пространственно-энергетически-временное распределение 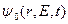нейтронов, инжектированных в бесконечно однородную среду точечным импульсным источником, приближенно можно представить в следующей мультипликативной форме:

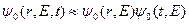, (8.146)

где 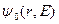— пространственно-энергетическое распределение нейтронов точечного стационарного источника, a 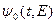— энергетически-временное распределение нейтронов от импульсных источников, равномерно заполняющих все пространство.

Факт строго формального разделения переменных (пространственных координат и времени) в представлении для 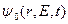,вообще говоря, не имеет места. Если бы равенство выполнялось строго, то величина 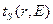полного времени замедления нейтронов до заданной энергии Е на заданном расстоянии r не зависела бы от пространственной переменной. Аналогично возраст нейтронов 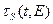, замедлявшихся до энергии Е за время t, в этом случае не зависел бы от величины t. 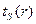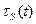В действительности зависимости и существуют, но оcи настолько слабы, что корреляцией между пространственно-энергетическим 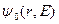и энергетически-временным 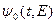распределением можно пренебречь. Специальные расчеты по методу Монте-Карло, проведенные для сред с различным водородосодержанием, подтверждают возможность использования приближенного соотношения (8.146) при всех временах, представляющих практический интерес [91].

Поскольку основные закономерности пространственно-энергетического распределения нейтронов стационарных источников рассмотрены выше, перейдем к анализу энергетически-временного распределения нейтронов в случае импульсного источника.

Для вещества произвольного состава и сечений взаимодействия, изменяющихся с энергией нейтронов, временное распределение замедленных нейтронов описывается гамма-распределением с плотностью

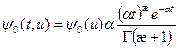. (8.147)

Параметры этого распределения 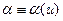и 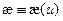определяются интегральными характеристиками кинетики замедления — полным временем замедления 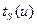и дисперсией импульса D[t(u)]:

;

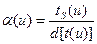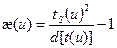. (8.148)

Эти параметры можно вычислять в различных спектральных приближениях [45]. Выражение (8.147) справедливо при практически неограничительном условии 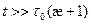в силу малости 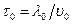. При малом водородосодержании 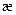>>1, 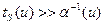, поэтому 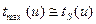и гамма-распределение переходит нормальное:

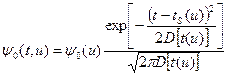. (8.149)

Изменение концентрации поглотителей влияет, главным образом, на амплитуду замедленных нейтронов.

В спектральном приближении Грюлинга — Гертцеля плотность столкновений 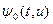замедленных нейтронов от импульсного источника в поглощающей среде произвольного состава с постоянными сечениями взаимодействия определяется выражением

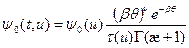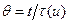; , (8.150)

где

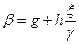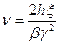, . (8.150 )

При отсутствии поглощения (g = 0) отсюда вытекают результаты, полученные В. Ф. Захарченко [28] и Ж. Коппелем. Результат спектрального приближения Вигнера получается из выражения (46), как частный случай при 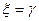, когда 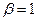, 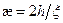(этот результат впервые получен И.Г.Дядькиным). В общем виде результат (8.147) получен Д.А.Кожевниковым.

Распределение (8.147) достигает максимума по истечении промежутка времени 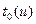, называемого временем собственно замедления.

Приближение Вигнера правильно определяет положение максимума временного распределения и удовлетворительно описывает увеличение плотности потока замедленных нейтронов при малых временах. Однако при временах, превышающих время собственного замедления 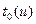,приближение Вигнера не согласуется с имеющимися экспериментальными данными, предсказывая значительно более сильное затухание импульса замедленных нейтронов в среде, чем это бывает в действительности. Причиной такого расхождения является неучет влияния неасимптотических отклонений функции Плачека.

Энергетически-временное распределение нейтронов практически не зависит от начальной энергии нейтронов и определяется характеристиками взаимодействия их со средой при фиксированной конечной энергии. Влияние неупругого рассеяния проявляется в уменьшении времени замедления и увеличении дисперсии импульса замедленных нейтронов. Но это влияние настолько слабо, что им практически можно пренебречь. Это значит, что энергетический спектр источника и неупругое рассеяние фактически не влияют на временное распределение замедленных нейтронов.

На рис.8.13 сопоставлены временные распределения плотности замедления 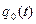нейтронов в кварцевом песчанике различной водонасыщенности, вычисленные методом Монте-Карло[4] с учетом энергетических зависимостей сечений взаимодействия, а также в спектральных приближениях Вигнера и Грюлинга — Гертцеля. Аналитический расчет в спектральном приближении Грюлинга — Гертцеля хорошо согласуется с результатами численных расчетов, тогда как приближение Вигнера дает удовлетворительный результат лишь в случае воды (напомним, что для чистого водорода оно совпадает с точным решением). Для воды распределение асимметрично, при отсутствии водорода, в соответствии с (8.149), оно имеет форму гауссоиды. То обстоятельство, что формулы, по которым производился аналитический расчет, получены в приближении постоянных сечений, а данные математического моделирования относятся к переменным сечениям, нисколько не ухудшает согласия теории с экспериментом. Это объясняется определяющим влиянием на временное распределение заключительной стадии процесса замедления, на которой сечения взаимодействия изменяются с энергией нейтронов сравнительно слабо.

Поскольку методом Монте-Карло обычно вычисляется не плотность потока замедленных нейтронов, а функционал от него — плотность замедления, временные распределения на рис.8.13 сравниваются в терминах плотности замедления. Рисунок иллюстрирует существенное различие временных распределений плотности замедления и плотности столкновений.

Одной из интересных особенностей кинетики замедления нейтронов является эффект так называемой «фокусировки» по энергии (более точно — монохроматизации спектра) в процессе замедления, поскольку дисперсия D[E(t)] энергетического распределения нейтронов со временем изменяется по закону 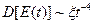, т. е. резко уменьшается со временем. В каждый фиксированный момент дисперсия тем меньше, чем меньше среднее изменение летаргии нейтронов в среде. Эта закономерность, наиболее сильно проявляющаяся в тяжелых средах, существенно используется в спектрометрах по времени замедления нейтронов и в спектрально-резонансном анализе вешества.

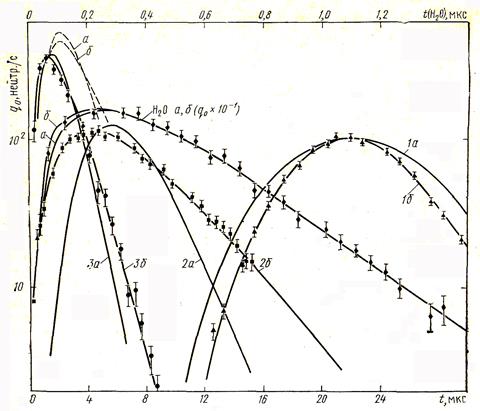
Рис.8.13. Зависимость плотности замедления от времени для нейтронов с энергией 5 эВ (импульсный источник 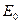=14 МэВ) для воды (верхняя шкала) и кварцевого песчаника с т=0 (1), с m=5 % (2), с m=20 % (3). Сопоставление результатов расчетов в спектральных приближениях Вигнера (а) и Грюлинга - Гертцеля (б) с даннымиматмоделированияпо методу Монте-Карло (точки). Пунктирные кривые соответствуют плотности столкновений