ЭНЕРГЕТИЧЕСКИЙ СПЕКТР НЕЙТРОНОВ ПРИ НАЛИЧИИ ПОГЛОЩЕНИЯ

Типы взаимодействий между нейтронами и атомными ядрами существенно опреде­ляются энергией нейтронов, поэтому значительное внимание приходится уделять теории нейтронного спектра в горных породах.

При поисках и разведке полезных ископаемых нейтронными методами как в полевых, так и в скважинных условиях могут использоваться спектральные эффекты, обусловленные резонансными рассеянием и поглощением нейтронов в процессе их замедления в горных породах.

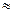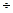При высоких энергиях (Е 10 14 МэВ) поглощение нейтронов в пороговых реакциях влияет на их распределение в горных породах. В области надтепловых энергий для горных пород и руд характерно присутствие сильно поглощающих элементов. Почти у всех породообразующих элементов в надтепловой области сечение поглощения растет с уменьшением энергии по закону 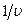. В резонансной области сечения поглощения ряда тяжелых (рудных) элементов достигают очень высоких значений, на несколько порядков (в тысячи и десятки тысяч раз) превосходящих величину сечений рассеяния.

Знание нейтронных спектров в горных породах необходимо также для изучения распределения гамма-излучения неупругого рассеяния, захватного гамма-излучения и активационных эффектов. Если энергетический спектр 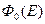замедленных нейтронов известен, то спектр 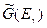гамма-излучения, возникающего при неупругом рассеянии нейтронов, определяется следующим образом:

,

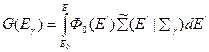где 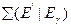— сечение испускания гамма-кванта энергии 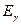при неупругом рассеянии нейтрона с энергией 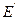. Аналогично вычисляется спектр G_a( 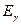) гамма-излучения, возникающего при поглощении нейтронов в процессе замедления:

,

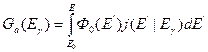где 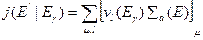— излучающая способность среды; 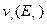— -число гамма-квантов данной энергии на один поглощенный данным ядром нейтрон; 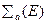— макроскопическое сечение поглощения нейтронов ядром типа 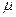,; суммирование ведется по ядрам всех элементов (изотопов) и всем линиям (l) в спектре каждого излучателя.

В физике биологической защиты от нейтронного облучения поглощенная или экспозиционная доза Д определяется выражением

,

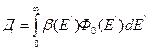где 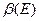— доза, создаваемая единичной плотностью потока нейтронов с фиксированной энергией Е.

В поглощающей среде плотность столкновений 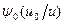нейтронов моноэнергетического источника с летаргией 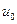удовлетворяет уравнению

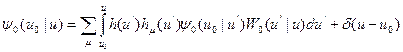, (8.120)

где 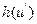— полная вероятность рассеяния, h(u) = 1—g(u)_; g(u) — полная вероятность поглощения; 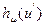— парциальная вероятность рассеяния на ядрах 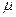-го элемента (суммирование распространяется на все элементы).

Решение этого интегрального уравнения в случае сильно изменяющихся с энергией нейтронов сечений рассеяния и поглощения представляет значительные трудности. Поэтому рассмотрим эквивалентную неканоническую форму этого уравнения [46], впервые полученную А. Вейнбергом и Е. Вигнером, Н. Корнголдом и В. В. Орловым:

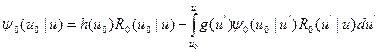. (8.121)

Здесь 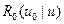— плотность столкновений нейтронов в среде без поглощения, т. е. 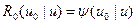при 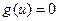[ 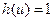]; функция 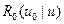называется функцией Плачека. В отличие от уравнения (28) в уравнении (28') спектр в поглощающей среде 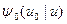выражается через спектр 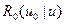,в среде без поглощения — через решение значительно более простой задачи. (Это обстоятельство является важным преимуществом неканонических форм уравнения переноса, преобразующихся в дифференциальные уравнения, обеспечивающие возможность нахождения их решений в аналитической форме для весьма сложных энергетических зависимостей сечений взаимодействия.)

Для среды, состоящей из одного элемента, функция Плачека 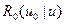обладает следующими свойствами. В интервале первого рассеяния 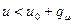, она экспоненциально возрастает, при 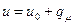имеет разрыв (в случае водорода разрыв отсутствует), при дальнейшем увеличении летаргии испытывает гармонические колебания с затухающей амплитудой около своего асимптотического значения 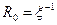( 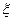— среднее изменение летаргии в одном столкновении), имеет разрыв производной по и при 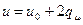, и при 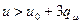достигает асимптотической величины. Можно строго показать, что в непоглощающей среде произвольного состава и при произвольной энергетической зависимости сечений рассеяния от энергии нейтронов уже после нескольких первых столкновений спектр имеет асимптотический вид

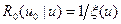, (8.130)

т. е. не зависит от начальной энергии нейтронов, но зависит от конечной энергии замедления.

Рис.8.8. Функция Плачека для водорода, углерода, кислорода и кальция; шкала летаргии – в единицах средней логарифмической потери энергии x для соответствующих элементов.

Переходя от плотности столкновений к измеряемой величине — плотности потока нейтронов 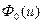, получаем

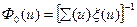= æ 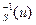, (8.130)

где æ 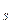(u) —замедляющая способность среды.

Следовательно, энергетическое распределение замед­ленных нейтронов при отсутствии поглощения имеет следующий вид:

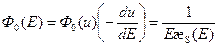. (8.130 )

Поскольку замедляющая способность среды при E>50 кэВ существенно зависит от энергии, спектр нейтронов, вообще говоря, отличается от 1/Е. Точнее, на фермиевский закон 1/Е, определяющий общий характер спектра, накладывается локальная «тонкая» структура, обусловленная резонансным характером зависимости полного сечения рассеяния от энергии нейтронов. Из выражения (8.130') следует, что резонансным максимумам сечения рассеяния соответствуют провалы (депрессии) в спектре нейтронов, а интерференционным минимумам сечения — «всплески» плотности потока нейтронов. (Это важное свойство присуще энергетическому спектру замедленных нейтронов не только в чисто рассеивающих средах, но и в поглощающих.)

Вернемся к изучению спектра замедленных нейтронов в поглощающих средах. Используя свойства функции Плачека 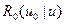, представим ее в виде разности асимп­тоти­ческого (соответствующего большим значениям летаргии) значения 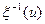и осцил­лиру­ющей добавки 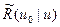,которая отлична от нуля лишь в интервале первых трех-четырех столкновений:

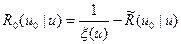. (8.131)

Подставив (8.131) в уравнение (8.120), получим

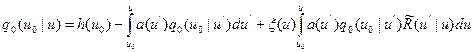, (8.132)

Где 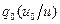- называется плотностью замедления:

; .

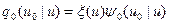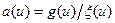Для решения этого уравнения применим метод, который назовем методом спектральных приближений. Последовательные приближения в этом методе соответствуют последовательно возрастающей точности, с которой учитываются неасимптотические свойства функции Плачека.

В первом спектральном приближении примем 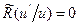, т. е. откажемся от учета осцилляции функции Плачека. Интегральное уравнение (32) сводится к дифференциальному уравнению первого порядка типа Бернулли, решение которого с начальным условием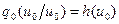

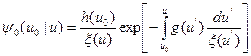(8.133)

совпадает с известным в теории резонансного поглощения приближением Вигнера. В случае поглощения при замедлении в чистом водороде оно дает точный результат и служит хорошим приближением при хорошо разрешенных резонансных сечениях поглощения, когда ширина резонанса мала по сравнению с интервалом однократного рассеяния, а расстояния между резонансами превышают несколько таких интервалов. Спектральное приближение Вигнера является исходным при определении резонансного интеграла поглощения.

Для вычисления следующего спектрального приближения воспользуемся тем обстоятельством, что функция 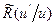отлична от нуля лишь в малой окрестности верхнего предела интегрирования в уравнении (8.132), и вынесем произведение 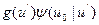за знак интеграла со значением в верхнем пределе:

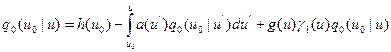, (8.134)

где

.

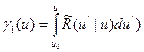Это интегральное уравнение также сводится к дифференциальному (уравнение Бернулли), решение которого имеет вид

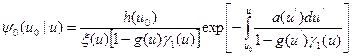(8.135)

Неудобство использования этого спектрального приближения обусловлено необходимостью численного расчета величины 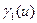для каждой конкретной среды. Однако если вблизи конечной энергии замедления парциальные вероятности рассеяния не зависят (или слабо зависят) от энергии нейтронов, величина 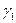не зависит от летаргии и представима в удобном для расчетов виде:

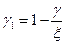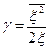; ; (8.136)

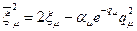. (8.137)

Требование постоянства парциальных вероятностей рассеяния означает, что сечения рассеяния нейтронов на ядрах различных элементов, входящих в состав среды, или не зависят от энергии нейтронов, или изменяются с энергией по одному и тому же закону. Для сред, не содержащих водород (или содержащих его в очень малом количестве), 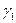>0, а для водородсодержащих сред при m>l % 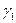>0. При добавлении водорода в смесь тяжелых ядер параметр 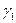меняет знак и достигает величин, по модулю гораздо больших 1/3. Объясняется это тем, что при добавлении водорода само асимптотическое решение убывает гораздо быстрее (за счет резкого увеличения средней логарифмической потери энергии в среде), чем уменьшаются неасимптотические отклонения от фермиевского спектра.

Подставив выражение (8.136) в (8.135), получим:

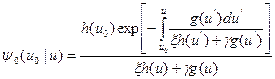. (8.138)

Этот результат совпадает с так называемым приближением Грюлинга — Гертцеля. Процесс вычисления спектральных приближений можно продолжить, но результаты уже потеряют наглядность.

Из выражений (8.133) и (8.138) следует, что энергетический спектр нейтронов в поглощающей среде можно записать в виде произведения спектра нейтронов в среде без поглощения 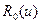на вероятность 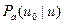избежать поглощения при замедлении до заданной летаргии:

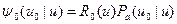. (8.139)

В случае 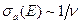хорошо выполняется условие применимости спектрального приближения Грюлинга — Гертцеля. Поскольку при начальной энергии нейтронов порядка единиц мегаэлектронвольт поглощением можно пренебречь, выражение для спектра плотности потока нейтронов 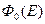имеет сле­дующий вид:

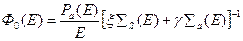, (8.140)

где 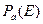— вероятность избежать поглощения при замедлении до энергии Е:

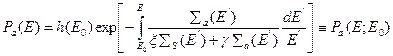(8.141)

Для полиэнергетического источника соответствующая величина

.

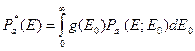Интеграл в выражении (8.141) можно вычислить аналитически при условии, что сечение рассеяния не зависит (или слабо зависит) от энергии. Полагая 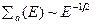, находим

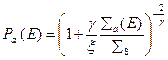. (8.141 )

Подставив (8.141') в (8.140), окончательно получим

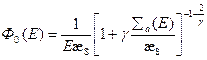. (8.142)

Требование постоянства сечения рассеяния ограничивает область применимости выражения (8.142). В реальном случае сечений рассеяния, зависящих от энергий нейтронов (в резонансной области), при 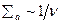величина 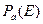по-прежнему монотонно зависит от энергии нейтронов, однако энергетический: спектр 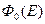приобретает тонкую структуру, обусловленную резонансами сечения рассеяния. Тем не менее, результат, полученный в приближении 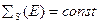, практически весьма полезен при изучении влияния присутствия поглощающих элементов на распределение замедленных нейтронов, поскольку при энергиях менее 50 кэВ сечение рассеяния для породообразующих элементов, как правило, слабо зависит от энергии.

Для водородсодержащих сред ( 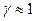) хорошим приближением служит более простая формула:

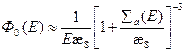. (8.143)

Отметим, что параметр 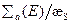представляет собой (с точностью до постоянного множителя) отношение двух характеристических параметров импульсного режима времени собственно замедления и времени жизни нейтронов относительно поглощения при конечной энергии замедления:

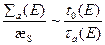, (8.144)

поскольку

; .

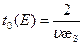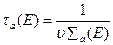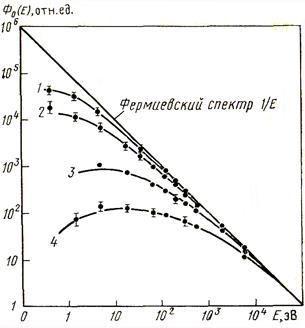
На рис.8.9 приведены результаты наиболее тщательных измерений спектра нейтронов в различных средах. Как видно, с уменьшением энергии нейтронов, когда сечение поглощения увеличивается, возрастает и отклонение от фермиевского спектра 1/E,устанавливающегося в среде без поглощения.

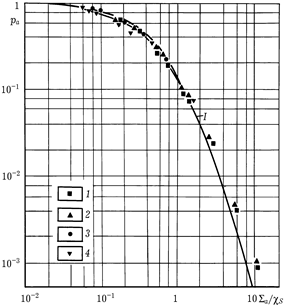
Рис.8.9. Энергетические спектры, нейтронов в поглощающих средах и в средах без поглощения; (по В. Н. Аваеву). Экспериментальные данные сопоставлены с расчетами в спектральном приближении Грюлинга — Гертцеля: 1 — смесь полиэтилена, железа и бора; 2 — спектр в железе; 3, 4 — смесь полиэтилена и карбида бора в различных концентрациях.

Рис.8.10. Уменьшение плотности потока нейтронов в веществах с поглощением по закону 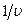относительно плотности потока в тех же средах при чистом рассеянии (по В. Н. Аваеву). Экспериментальные данные соответствуют измерениям в следующих средах: 1 — смесь железа с карбидом бора; 2 — смесь графита с бором; 3 — железо; 4 — смесь железа с полиэтиленом и карбидом бора. Ι — расчет в спектральном приближении Грюлинга — Гертцеля; ΙΙ (1,,2,3,4) – расчет в спектральном приближении Вигнера.

Влияние концентрации поглотителя на величину плотности потока нейтронов иллюстрирует рис.8.10, на котором показана зависимость отношения плотности потока нейтронов 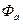в поглощающей среде к плотности потока 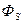в той же среде без поглощения от параметра 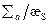при различных энергиях нейтронов). Приближение Грюлинга — Гертцеля значительно лучше согласуется с экспериментальными данными. Некоторое расхождение расчетной кривой с экспериментальными точками в области сильных поглощений объясняется пространственной зависимостью плотности потока замедленных нейтронов. На малых расстояниях от источника энергетическое распределение нейтронов определяется спектром 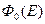, устанавливающимся в среде с равномерно распределенными источниками. Однако с увеличением поглощения пространственная зависимость функции пространственно-энергетического распределения нейтронов усиливается, что и приводит к отклонению измеренного спектра от пространственно-однородного.

Знание спектра замедленных нейтронов, не зависящего от координат (для равномерно распределенных источников), позволяет правильно описывать основные спектральные закономерности поля, образованного локализованным моноэнергетическим источником. Однако в случае локализованного источника происходит пространственное изменение спектра.

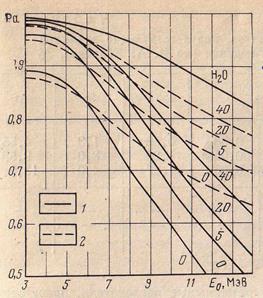
В горных породах при энергиях нейтронов Е>3—4 МэВ идут реакции с вылетом заряженных частиц, приводящие к поглощению нейтронов, поэтому с увеличением энергии нейтронов вероятность избежать поглощения в процессе замедления уменьшается и тем сильнее, чем меньше водородосодержание среды (рис.2.23, 2.24). В области надтепловых энергий величина 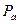возрастает при наличии поглотителей типа 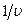. Но и в этом случае 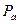тем меньше, чем меньше водородосодержание [102].

Если в замедлителе присутствуют резонансные поглотители, величину 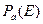в приближении Вигнера можно преобразовать к виду, удобному для оценки влияния резонансного поглощения на энергетический спектр нейтронов.

Величина показателя экспоненты в выражении (8.140) для вероятности избежать поглощения в процессе замедления

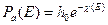(8.145)

определяется не только величиной, но и характером энергетической зависимости макроскопического сечения поглощения и замедляющей способности среды:

.

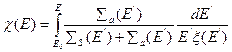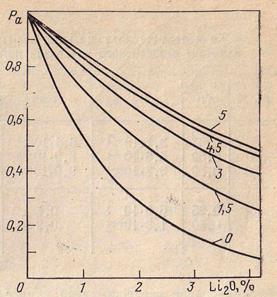
Рис.8.11. Вероятность избежать поглощения при замедлении в песчанике и известняке в зависимости от начальной энергии нейтронов (E=0,1 эВ) (по данным А. Крефта, с дополне­ни­ями). 1 — песчаник; 2 — известняк. Шифр кри­вых — объемная водонасыщенность m в %.	Рис.8.12. Зависимость вероятности избежать поглощения при замедлении от содержания окиси лития в пегматите (по Е. И. Крапивскому). Шифр кривых — влажность пегматита в %. Источник Ро—Be.