Радиус замедления нейтронов

На основании , полное число нейтронов с заданной энергией Е, замед­лившихся в объеме, ограниченном сферической поверхностью радиуса R, равно

,

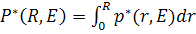а число нейтронов с энергией Е во всем бесконечном объеме замедлителя будет

.

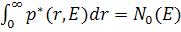Поскольку длина замедления нейтронов – конечная величина, процесс замедления нейтронов развивается в конечном объеме бесконечного замедлителя, ограниченном сферической поверхностью некоторого радиуса, центр которой совпадает с расположением источника нейтронов.

Величина отношения δ(R,E)

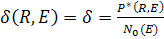; (0 ≤ δ ≤ 1);

показывает, какая часть от общего числа нейтронов с данной энергией Е замедляется в сферическом объеме V(R), ограниченном поверхностью заданного радиуса R.

Поставим вопрос: каков радиус R_S(E) такого сферического объема, в котором замедляется до заданной энергии Е подавляющая часть, например, 95% всех нейтронов (d=0,95).

Величина R_S(E), которую будем называть радиусом замедления, находится из уравнения

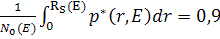5. (8.119)

Подставляя сюда (8.110), находим:

R_S(E) ≈ 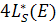, (8.120)

то есть радиус замедления равен четырем длинам замедления.

Таким образом, пространственное распределение нейтронов точечного источника в однородном замедлителе, ограниченном сферической поверхностью, радиус которой превышает радиус замедления, совпадает с распределением замедленных нейтронов в бесконечной однородной среде.