Индикатриса рассеяния

Индикатриса упругого рассеяния нейтронов в веществе определяется законами сохранения энергии и импульса в системе координат, жестко связанной с центром инерции системы «нейтрон - ядро-мишень» («система центра инерции»). Экспериментальные измерения проводятся в системе координат, в которой до рассеяния ядра замедлителя неподвижны («лабораторная» система). В соответствии с этим необходимо индикатрису рассеяния также выразить в лабораторной системе координат.

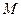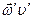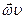Если выбрать в качестве единицы измерения массы ядра - мишени массу нейтрона, выразить скорость нейтрона в лабораторной системе координат до и после рассеяния в виде и , то, пользуясь законами сохранения энергии и импульса при упругом рассеянии, можно получить следующие выражения для угла рассеяния нейтронов в координатах системы центра инерции и в лабораторной системе координат:

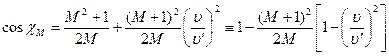, (7.55)

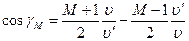. (7.56)

Из выражения (272) видно, что максимальная потеря скорости нейтрона происходит при «лобовом» ударе ( 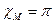, когда 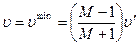), а также, что отношение скоростей (энергии) нейтрона до и после рассеяния не зависит от скорости (энергии) перед столкновением, а определяется лишь массой ядра - мишени 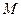. Последнее обстоятельство используется в формальном аппарате теории замедления, так как позволяет ввести новую переменную 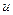, характеризующую энергию нейтрона), и называемую летаргией (или логарифмической энергией):

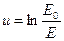, (7.57)

где 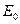и 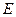- начальная и текущая кинетическая энергии нейтрона. Поскольку масса нейтрона совпадает с массой протона (ядра водорода), при упругом рассеянии водород оказывается аномально сильным замедлителем среди всех других элементов.

Величина потери энергии нейтронов, выраженная в единицах 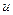, в результате столкновения не зависит от их энергий перед столкновением. Введение летаргии позволяет сжать чрезвычайно широкую область энергий, в которой происходит процесс замедления ( 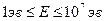), в значительно более обозримый интервал изменения переменной ( ).

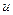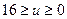С новой переменной выражения (272) и (273) принимают вид:

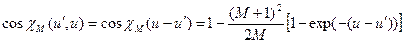, (7.58)

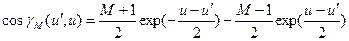. (7.59)

Максимальное увеличение летаргии в одном столкновении 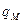равно:

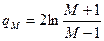. (7.60)

В каждом столкновении изменение летаргии нейтронов заключено в пределах

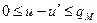. (7.61)

При изотропном рассеянии в системе центра инерции, характерном для нейтронов с энергией, равной сотням keV, плотность вероятности рассеяния нейтронов в заданный телесный угол 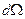будет равна:

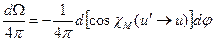, (7.62)

где, в соответствии с формулой (7.58),

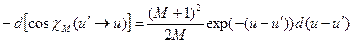. (7.63)

Плотность вероятности 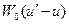рассеяния с заданным изменением летаргии получим, разделив выражение (7.63) на величину изменения летарги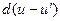и и :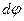

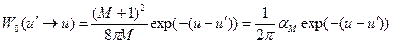, (7.64)

где обозначено

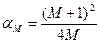. (7.65)

Чтобы перейти от величины 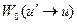к индикатрисе рассеяния 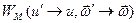, надо учесть, что равенство (7.64) справедливо лишь тогда, когда 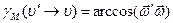, так как нарушение этого равенства означает отсутствие столкновения с ядром. С этой целью величину 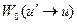необходимо умножить на дельта-функцию Дирака 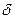от аргумента :

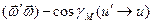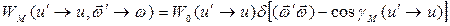. (7.66)

С полученным выражением для индикатрисы рассеяния, уравнение переноса нейтронов приводится к виду:

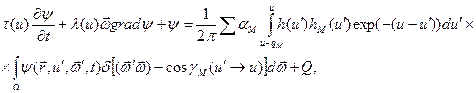(7.67)

где среднее время свободного пробега между двумя столкновениями

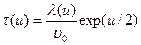. (7.68)

Функции распределения 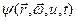и 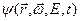связаны соотношением: 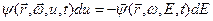, откуда

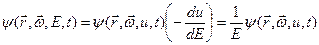. (7.69)