Свойства элементарных функций алгебры логики
Функции И, ИЛИ, НЕ в совокупности с логическими переменными (число их не менее 2; 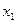 ,
, 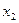 ) образуют булеву алгебру.
) образуют булеву алгебру.
Для неё справедливы аксиомы:
1. 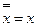
2. 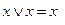 ,
, 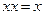 (идемпотентность)
(идемпотентность)
3. 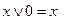 ,
, 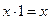
4. 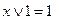 ,
, 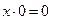
5. 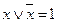 ,
, 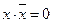
6. 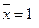 ,
, 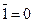
Для булевой алгебры справедливы свойства:
1) ассоциативность
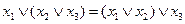 ;
;
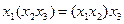 ;
;
2) коммутативность
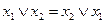 ;
; 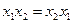 ;
;
3) дистрибутивность
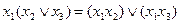 ;
;
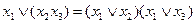 .
.
Для булевой алгебры справедливы законы де Моргана:
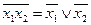 ;
; 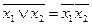
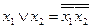 ;
; 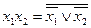
Докажем, например, закон де Моргана 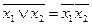
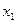
| 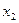
| 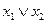
| 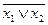
| 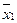
| 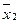
| 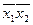
|
Для булевой алгебры справедливы законы поглощения и склеивания.
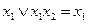 ;
; 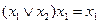 - поглощение
- поглощение
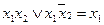 ;
; 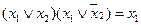 - склеивание
- склеивание
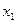
| 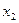
| 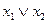
| 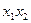
| 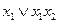
| 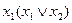
| 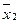
| 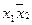
| 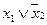
| 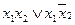
| 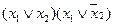
|
Свойства, аксиомы и теоремы булевой алгебры обладают дуальностью (т.е. функция И дуальна функции ИЛИ, а “1” дуальна “0”). При отсутствии в логическом выражении скобок первыми должны выполняться операции НЕ, затем И и последними – ИЛИ.
Пример:
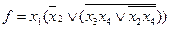 найти его отрицание и проверить с помощью закона де Моргана.
найти его отрицание и проверить с помощью закона де Моргана.
1. 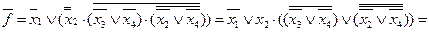
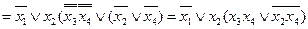
2. 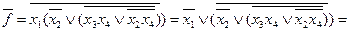
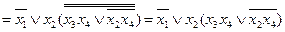
Рассмотрим теперь алгебру Жегалкина, состоящей из операций И, 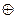 и операции константа 1. Для неё справедливы такие свойства.
и операции константа 1. Для неё справедливы такие свойства.
1. 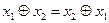 ,
, 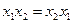 (коммутативность)
(коммутативность)
2. 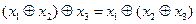 ,
, 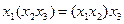 (ассоциативность)
(ассоциативность)
3. 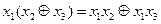 (дистрибутивность)
(дистрибутивность)
Для неё справедливы аксиомы:
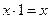
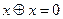
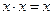
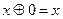
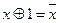
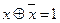
В алгебре Жегалкина нет принципа дуальности.
Связь между алгебрами Буля и Жегалкина устанавливается с помощью таких тождеств:
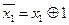 ;
; 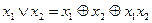 ;
;
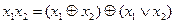 ;
; 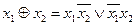
Дата добавления: 2016-07-18; просмотров: 2272;











