Глава 5. Формулировка задачи о течении и теплообмене в круглых трубах
Особенности численных методик, их достоинства и недостатки легко уяснить на ряде примеров течений, наиболее распространенных в практических приложениях. Некоторые их таких движений происходят в условиях геометрии и режимах, описанных в п. 5.1. Остановимся на этих процессах подробнее.
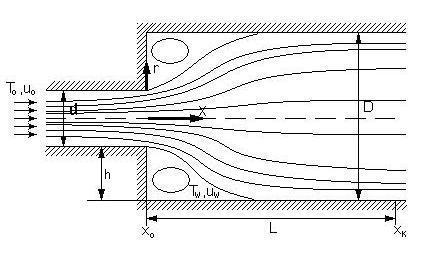 5.1 Физическая постановка задачи. Часто предполагается, что течения вязких сред (несжимаемой жидкости или слабосжимаемого газа) в трубопроводах неустановившиеся или стационарные, развивающиеся или развитые, ламинарные или турбулентные, неизотермические или изотермические. Кроме того, будем считать, что область движения имеет особенности, связанные с изменением формы поперечного сечения по длине трубопровода. В этом случае, на участках со скачком площади поперечного сечения образуются зоны, существенно влияющие на интенсивность обмена теплом, импульсом и массой со стенками. Качественную картину подобного течения иллюстрирует рис. 5.1, где хорошо видны зонные особенности.
5.1 Физическая постановка задачи. Часто предполагается, что течения вязких сред (несжимаемой жидкости или слабосжимаемого газа) в трубопроводах неустановившиеся или стационарные, развивающиеся или развитые, ламинарные или турбулентные, неизотермические или изотермические. Кроме того, будем считать, что область движения имеет особенности, связанные с изменением формы поперечного сечения по длине трубопровода. В этом случае, на участках со скачком площади поперечного сечения образуются зоны, существенно влияющие на интенсивность обмена теплом, импульсом и массой со стенками. Качественную картину подобного течения иллюстрирует рис. 5.1, где хорошо видны зонные особенности.
Рис 5.1. Схема течения в области канала с внезапным расширением.
Заметим, что предсказание структуры потока, механизмов конвективно-диффузионного взаимодействия в этих областях весьма важно для проектировщиков. Эти детали позволяют правильно оценить потери на трение и теплоотдачу к стенкам и корректно рассчитать наиболее оптимальный режим транспорта природного сырья по трубопроводу. Учтем данные положения в физической модели течения, а также, что течение осесимметричное в отсутствии действия внешних сил, наличия объемных источников тепла. Однако, считаем, что температурные перепады на отдельных участках могут быть значительными, а, следовательно, заметно меняются теплофизические свойства рабочей среды от температуры. Предполагаем далее, что из трубы диаметра d однородный поток поступает в трубу с большим диаметром D со скоростью 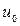 и температурой
и температурой 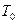 . Допускается, что предвключенный участок с диаметром d достаточно протяженный. Тогда на входе в большой канал поток будет иметь (для простоты изложения) развитый профиль скорости Хагена-Пуазейля:
. Допускается, что предвключенный участок с диаметром d достаточно протяженный. Тогда на входе в большой канал поток будет иметь (для простоты изложения) развитый профиль скорости Хагена-Пуазейля:
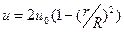 . (5.1)
. (5.1)
На стенках канала задан тепловой поток qw или температура 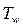 , не равная температуре потока
, не равная температуре потока 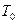 . Имеется прилипание частиц жидкости к твердой стенке. Это означает отсутствие скорости скольжения жидкости по поверхности. Таким образом, выполняется граничное условие равенства нулю скорости жидкости на поверхности неподвижных стенок
. Имеется прилипание частиц жидкости к твердой стенке. Это означает отсутствие скорости скольжения жидкости по поверхности. Таким образом, выполняется граничное условие равенства нулю скорости жидкости на поверхности неподвижных стенок 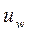 . Считается, что длина канала L достаточно протяженная, чтобы на выходе течение было развитым.
. Считается, что длина канала L достаточно протяженная, чтобы на выходе течение было развитым.
В таких условиях инженеру–вычислителю могут быть поставлены цели: а) построить и протестировать вычислительный алгоритм расчета устойчивых и переходных ламинарных и турбулентных неизотермических течений с особенностью границы области движения; б) оценить эффективность методики предсказания динамических и тепловых локальных и интегральных параметров течения и теплообмена, опираясь на сравнения с имеющимися опытными данными; в) исследовать влияния геометрии канала, высоты уступа, режима, скорости течения на область отрыва, присоединения потока, интенсивность и структуру вихреобразования. Данные положения следует формализовать с математической точки зрения.
5.2 Математическая формулировка проблемы.Система дифференциальных уравнений, определяющая теплообмен при турбулентном течении однородного инертного потока слабосжимаемого газа в канале с изотермической стенкой включает уравнения: неразрывности, осредненные уравнения Навье – Стокса (динамические уравнения Рейнольдса), энергии, которые в тензорной форме были представлены выше и имеют вид:
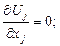 (5.2)
(5.2)
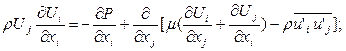 (5.3)
(5.3) 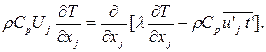 (5.4)
(5.4)
Переменность теплофизических свойств от температуры определяется зависимостью Саттерленда:
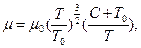 (5.5)
(5.5)
где  – динамический коэффициент вязкости при нормальных условиях
– динамический коэффициент вязкости при нормальных условиях 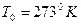 ; T – локальная температура; С – эмпирическая постоянная для закона (5.5), отвечающая конкретной газообразной среде. В случае анализа жидких капельных сред переменность теплофизических свойств учитывается формулой Рейнольдса-Филонова:
; T – локальная температура; С – эмпирическая постоянная для закона (5.5), отвечающая конкретной газообразной среде. В случае анализа жидких капельных сред переменность теплофизических свойств учитывается формулой Рейнольдса-Филонова:
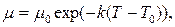 (5.6)
(5.6)
где k – опытная константа.
Заметим, что в случае анализа ламинарного режима течения и теплообмена система (5.2) – (5.4) вырождается в систему уравнений Навье – Стокса и энергии с напряжениями  ,
, 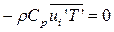 , для решения которых используются технологии, сообщенные выше. При турбулентных процессах систему (5.2) - (5.4) необходимо дополнить зависимостями, определяющими коэффициенты турбулентного обмена
, для решения которых используются технологии, сообщенные выше. При турбулентных процессах систему (5.2) - (5.4) необходимо дополнить зависимостями, определяющими коэффициенты турбулентного обмена 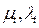 .
.
5.3. Модель турбулентности к замыканию уравнений, определяющих течение и теплоперенос во внутренних системах.Учитывая замечания к моделированию турбулентности, высказанные во введении, остановимся на моментной теории и многопараметрических (двухпараметрических тепловых и динамических) моделях. Тогда для напряжений Рейнольдса и турбулентных потоков тепла по подходу Колмогорова – Прандтля будем иметь:
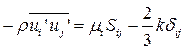 ; (5.7)
; (5.7)
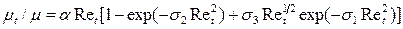 ; (5.8)
; (5.8)
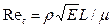 ; (5.9)
; (5.9)
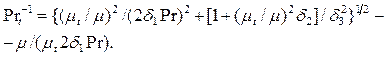 (5.10)
(5.10)
Замыкание определяющих уравнений проводится по K – L – модели, так как она более экономична при получении решения и эффективна в описании низкорейнольдсовых процессов. Ее транспортные уравнения имеют вид:
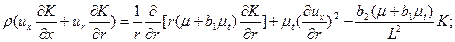 (5.11)
(5.11)
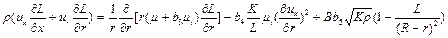 . (5.12)
. (5.12)
Значения констант в k-L модели следующие:
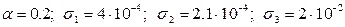 ;(5.14)
;(5.14)
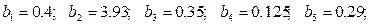
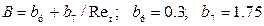 . (5.13)
. (5.13)
В определении турбулентных тепловых потоков  также используются двухпараметрические модели, представляющие уравнения для автокорреляций пульсаций температуры (энтальпии), скорости ее диссипации и имеют структуру, подобную уравнениям (5.11), (5.12):
также используются двухпараметрические модели, представляющие уравнения для автокорреляций пульсаций температуры (энтальпии), скорости ее диссипации и имеют структуру, подобную уравнениям (5.11), (5.12):
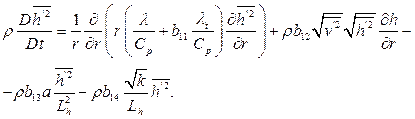 |
(5.14)
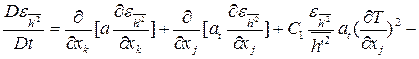
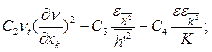 (5.15)
(5.15)
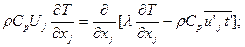 (5.16)
(5.16)
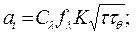 (5.17)
(5.17)
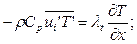 (5.18)
(5.18)
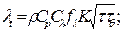 (5.19)
(5.19)
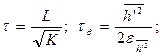 (5.20)
(5.20)
5.4 Краевые условия. Для осредненных и пульсационных гидродинамических характеристик необходимые краевые условия к интегрированию определяющих уравнений имеют вид (см. рис. 5.2):
1. На оси 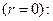 условия симметрии
условия симметрии 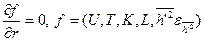 ;
;
2. На входе 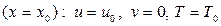 ,
, 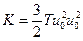 , где
, где
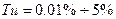 – интенсивность турбулентности, интегральный масштаб турбулентности
– интенсивность турбулентности, интегральный масштаб турбулентности 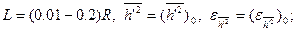
3. На стенке 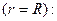 выполняются условия прилипания, как для осредненных, так и пульсационных характеристик
выполняются условия прилипания, как для осредненных, так и пульсационных характеристик 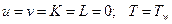 ;
; 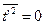 ;
; 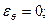
4. На выходе 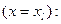
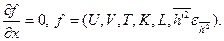
|
Дата добавления: 2020-07-18; просмотров: 746;











