Особенности используемого численного метода и алгоритм решения задач теплообмена.
Представленный в данном разделе численный алгоритм отличается спецификой, которую вносит априорная информация о характере течения среды у стенки. Существование в пристеночной зоне трубопровода высоких поперечных градиентов искомых величин заставляет работать с неравномерными сетками. Кроме того, мы учитываем положительные моменты, которые дают маршевые методы и способы одновременного нахождения поля скорости и градиента давления. Поэтому сформулируем методику, широко апробированную на расчете внутренних течений, дающую удовлетворительные результаты анализа прямоточных и закрученных инертных и химически реагирующих систем в трубах.
Итак, в алгоритме используем сетки со сгущением узлов в особых областях (стенка-ядро), итерационные методы, экономичные неявные конечно-разностные схемы, а также схемы расщепления по физическим процессам. Специфика расщепления будет заключаться в следующем. При малой интенсивности закрутки и небольших скачках площади поперечного сечения канала (tgα<0.1, где α – угол наклона боковой поверхности к оси течения) используется маршевый способ построения решения. Далее этот алгоритм может быть обобщен на режимы с закруткой высокой интенсивности и умеренные размеры скачка сечения, но суть его, по-прежнему, будет заключаться в выделении маршевой переменной и способе одновременного с полем скорости нахождения градиента давления. В такой формулировке мы имеем версию, обобщения идей Л.М. Симуни [5, 8, 12] на случай переменного по сечению канала давления. Как показывает наш опыт, в классе осесимметричных задач построенный численный алгоритм по быстродействию не будет уступать алгоритмам численногоинтегрирования уравнений двумерного пограничного слоя.
5.5.1. Схема численного интегрирования уравнений приближения “узкого канала”.При решении осесимметричных задач о течении вязкой несжимаемой жидкости в каналах постоянного и слабоменяющегося сечения в отсутствие влияния объемных сил используется следующая система уравнений импульсов и энергии:
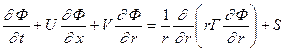 . (5.5.1)
. (5.5.1)
Т а б л и ц а 1
Коэффициенты обобщенного уравнения (5.5.1).
| Ф | Г | S | ||
| U | n | -(¶P/¶x)/r | ||
| 0 | n | -(¶P/¶r)/r-W2/r | ||
| W | n | -VW/r-nW/r2 | ||
| T | a |
Здесь n=m/r - коэффициент кинематической вязкости, a=l¤(rсP) – коэффициент температуропроводности.
Рассмотрим ключевые моменты в способе получения численного решения в этом случае. Уравнение (5.5.1) перепишем следующим образом:
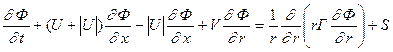 . (5.5.2)
. (5.5.2)
Представление конвективного члена в форме (5.5.2) позволяет реализовать двухстадийную схему получения решения, причем на первой стадии корректным образом осуществить маршевую процедуру расчета, связанную с последовательным продвижением в положительном направлении оси Ox. Это возможно, поскольку коэффициент (U+|U|) при ¶Ф/¶x всегда неотрицателен даже при наличие в потоке интенсивных возвратных движений.
Рассмотрим аппроксимацию отдельных членов уравнения (5.5.2). Эволюционный член представим следующим образом:
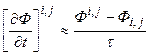 . (5.5.3)
. (5.5.3)
Здесь и ниже верхнее расположение двойных индексов будет отвечать верхнему слою по времени, нижнее – нижнему, индекс i соответствует выделенному сечению по длине канала, j отмечает положение при продвижении вдоль радиальной координаты, t - шаг по времени.
По возможности будем ориентироваться на разработку неявных схем, поэтому ниже все пространственные производные будут расписаны с использованием сеточных значений функций на верхнем слое по времени. В связи с этим, аппроксимация (5.5.3) представляет собой одностороннюю разность по времени и имеет первый порядок точности относительно t. Все производные по радиальной координате будут аппроксимированы со вторым порядком точности относительно шага Dr, а производные по продольной – с первым относительно шага Dx. Сеточный шаблон, на котором расписаны пространственные производные, имеет следующий вид.
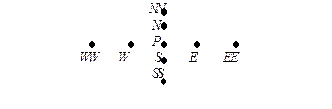
| Рис. 5.3. Сеточный шаблон, используемый для записи разностного аналога уравнения (5.5.2). |
Выпишем все необходимые аппроксимации:
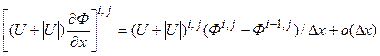 , (5.5.4)
, (5.5.4)
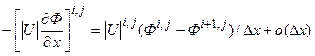 , (5.5.5)
, (5.5.5)
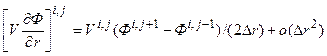 , (5.5.6)
, (5.5.6)
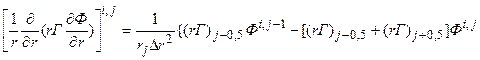 +
+
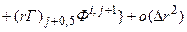 , (5.5.7)
, (5.5.7)
где 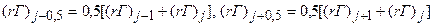 .
.
Далее введем обозначения:
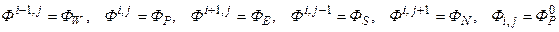 .
.
Тогда разностный аналог, отвечающий уравнению (5.5.2) будет выглядеть следующим образом:
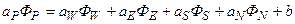 , (5.5.8)
, (5.5.8)
где 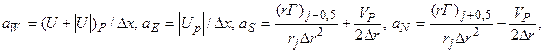
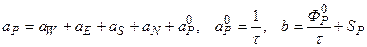 . (5.5.9)
. (5.5.9)
Разностное уравнение (5.5.8) будем решать итерационным методом при обязательном прохождении двух последовательных этапов:
(I) 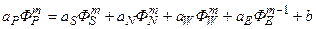 , (5.5.10)
, (5.5.10)
(II) 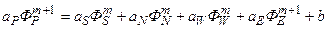 . (5.5.11)
. (5.5.11)
Здесь m – номер итерационного слоя. Рассмотрим подробнее первый этап вычислений. При однонаправленном во входном сечении движении жидкости значение субстанции Ф в этом сечении следует считать заданным. Мы уже упоминали, что при решении уравнений переноса на этапе (I) возможна реализация маршевой процедуры вычислений. Выполняя первый шаг этой процедуры найдем распределения Ф в первом сечении, далее во втором и т.д.
Таким образом, значения ФW , входящие в (5.5.10), всегда будут известны, а величину ФE на этом этапе берем с предыдущего итерационного слоя. Поэтому уравнения (5.5.10) можно переписать следующим образом:
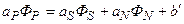 , (5.5.12)
, (5.5.12)
где 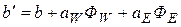 .
.
Система уравнений (5.5.12) может быть эффективно разрешена методом прогонки. При Ф = W, T из (5.5.12) получаются разностные уравнения, не содержащие градиента давления и их решение не связано с какими–либо сложностями. Остановимся на особенностях разрешения системы U-уравнений, полученной на основе (5.5.12). В эту систему уже входят неизвестные величины (¶P/¶x)p.
Для решения этой системы мы используем способ одновременного с полем скорости нахождения градиента давления. Следуя которому сеточные значения продольной компоненты вектора скорости записываются в виде, аналогичном [1], следующим образом:
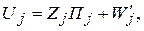 (5.5.15)
(5.5.15)
где 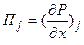 . Для простоты записи в (5.5.13) индекс i опущен. Отличие (5.5.13) от зависимости, предложенной в [1], состоит в том, что здесь сеточные значения П зависят не только от i, но и от j, то есть П является переменной по поперечному сечению величиной. Поэтому для определения продольного градиента давления недостаточно условия постоянства расхода и требуется некоторое уравнение, позволяющее его найти. В качестве такового используем уравнение количества движения в проекции на радиальное направление, разрешенное относительно поперечного градиента давления:
. Для простоты записи в (5.5.13) индекс i опущен. Отличие (5.5.13) от зависимости, предложенной в [1], состоит в том, что здесь сеточные значения П зависят не только от i, но и от j, то есть П является переменной по поперечному сечению величиной. Поэтому для определения продольного градиента давления недостаточно условия постоянства расхода и требуется некоторое уравнение, позволяющее его найти. В качестве такового используем уравнение количества движения в проекции на радиальное направление, разрешенное относительно поперечного градиента давления:
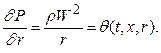 (5.5.14)
(5.5.14)
Соотношение (5.5.14) выражает баланс поверхностных и массовых сил (в данном случае центробежных). Дифференцируя его по x и строя подходящий разностный аналог, будем иметь:
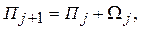 (5.5.15)
(5.5.15)
где 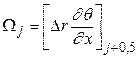 и Drj+1/2=rj+1-rj. Такое представление обеспечивает аппроксимацию с точностью до членов второго порядка малости относительно шага по радиальной координате.
и Drj+1/2=rj+1-rj. Такое представление обеспечивает аппроксимацию с точностью до членов второго порядка малости относительно шага по радиальной координате.
При Ф=U из (5.5.12) имеем
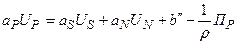 , (5.5.16)
, (5.5.16)
где 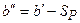
Подставляя в (5.5.16) зависимость (5.5.13), получим
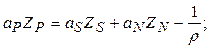 (5.5.17)
(5.5.17)
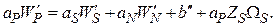 (5.5.18)
(5.5.18)
Используя связь (5.5.13) и формулу трапеций при вычислении интегрального потока массы, можно получить соотношение:
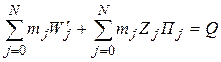 . (5.5.19)
. (5.5.19)
Здесь mj=2prrj Drj, узел N относится к оси течения, Q - расход жидкости через поперечное сечение канала.
Из (5.5.15) следует равенство
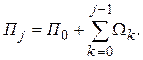 (5.5.20)
(5.5.20)
Тогда с использованием (5.5.19), (5.5.20) можем найти
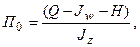 (5.5.21)
(5.5.21)
где 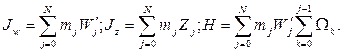 (5.5.22)
(5.5.22)
Зная величину продольного градиента давления на стенке П0 и используя рекуррентное соотношение (5.5.15), можно рассчитать значения 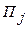 во всех точках поперечного сечения канала, которые необходимы для определения сеточных значений продольной компоненты скорости по (5.5.13). Величина поперечной компоненты скорости находится из уравнения неразрывности.
во всех точках поперечного сечения канала, которые необходимы для определения сеточных значений продольной компоненты скорости по (5.5.13). Величина поперечной компоненты скорости находится из уравнения неразрывности.
Мы уже ввели переменный шаг по поперечной координате при изложении способа одновременного с полем скорости нахождения градиента давления. Не составит большого труда построить разности (5.5.6), (5.5.7) применительно к этому случаю. Поэтому, здесь уместно сделать замечания, относящиеся к построению неравномерных сеток, которые будут полезны при рассмотрении задач о турбулентном закрученном течении.
При построении сгущающейся сетки у стенки и у оси канала используются преобразования вида:
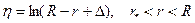 ;
; 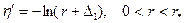 ,
,
где R - радиус канала, 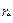 - точка, для которой принимается, что
- точка, для которой принимается, что 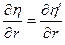 , т.е.
, т.е. 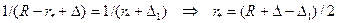 (*). Тогда
(*). Тогда 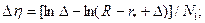
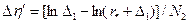 . Здесь N1, N2 - количество точек разностной сетки, определяющее общее число узлов по поперечной координате (NG): NG=N1+N2. Необходимо также потребовать, чтобы
. Здесь N1, N2 - количество точек разностной сетки, определяющее общее число узлов по поперечной координате (NG): NG=N1+N2. Необходимо также потребовать, чтобы 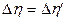 , т.е.
, т.е. 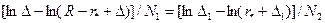 . Из последного соотношения находим
. Из последного соотношения находим 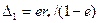 (**), где
(**), где 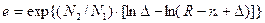 . Заметим, что
. Заметим, что 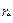 также зависит от D1, однако эта зависимость является слабой. Полагая в (**)
также зависит от D1, однако эта зависимость является слабой. Полагая в (**) 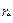 =R/2, сразу находим более или менее подходящее приближение для D1. Далее оно может быть уточнено простым пересчетом по формулам (*) и (**). Таким образом, задавая D, N1, N2, можно найти D1 и, соответственно, все элементы преобразования координат.
=R/2, сразу находим более или менее подходящее приближение для D1. Далее оно может быть уточнено простым пересчетом по формулам (*) и (**). Таким образом, задавая D, N1, N2, можно найти D1 и, соответственно, все элементы преобразования координат.
Замечания о сходимости итерационного процесса. Исходные уравнения нелинейны. Их линеаризация осуществляется сносом коэффициентов, содержащих значения искомой функции на предыдущий итерационный слой. Далее осуществляются как локальные, так и глобальные итерации. Сходимость итерационного процесса обеспечивается тем, что при реализации прогонок вдоль координатных линий мы стремимся обеспечить диагональное преобладание (хорошую обусловленность метода прогонки). В результате всегда выполняется критерий Скарбороу:
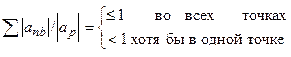 , (5.5.23)
, (5.5.23)
где 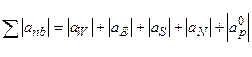 [см. (5.5.9)].
[см. (5.5.9)].
Из (9) следует, что для того, чтобы выполнялось правило положительной определенности коэффициентов необходимо, чтобы сеточное число Рейнольдса, определенное по поперечной компоненте скорости и шагу по радиальной координате, было меньше 2. Это ограничение не является слишком жестким, т.к. в рамках рассматриваемого класса задач величина V значительно меньше U, абольшие градиенты по r требуют использования мелкого шага по поперечной координате.
Разностная аппроксимация и схема интегрирования полных уравнений Навье-Стокса. Далее рассмотрим процедуру расчета закрученного течения жидкости в канале с резким расширением площади поперечного сечения. В этом случае следует опираться на систему полных уравнений Навье-Стокса. Обобщенное уравнение, отвечающее этой системе, выглядит следующим образом:
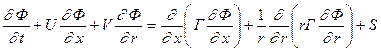 . (5.5.24)
. (5.5.24)
Значения коэффициентов Г и S даются приводимой ниже таблицей.
Таблица 2.
Коэффициенты обобщенного уравнения (24).
| Ф | Г | S | ||
| U | n | -(¶P/¶x)/r | ||
| V | n | -(¶P/¶r)/r+W2/r -nV/r2 | ||
| W | n | -VW/r-nW/r2 | ||
| T | a |
Описанный выше алгоритм решения уравнений движения, записанных в приближении “узкого канала”, может быть обобщен на случай полных уравнений Навье-Стокса. Обобщенное уравнение (5.5.24) представим аналогично (5.5.2) следующим образом:
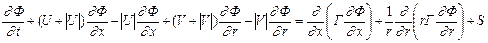 . (5.5.25)
. (5.5.25)
Для того, чтобы записать разностный аналог этого уравнения используем аппроксимации (5.5.5) – (5.5.9), а также разностные представления вновь введенных членов:
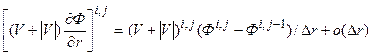 , (5.5.28)
, (5.5.28)
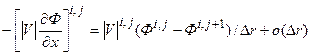 , (5.5.29)
, (5.5.29)
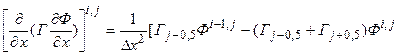 +
+
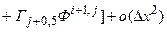 . (5.5.30)
. (5.5.30)
Тогда разностный аналог, отвечающий уравнению (5.5.27), будет иметь вид:
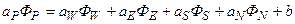 , (5.5.31)
, (5.5.31)
где 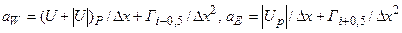 ,
,
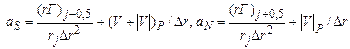 ,
,
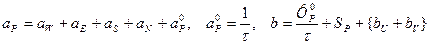 . (5.5.32)
. (5.5.32)
Видим, что все коэффициенты безусловно положительны. С помощью введенных в источниковый член “b” [см. (5.5.32)] добавок следующего вида:
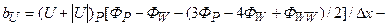
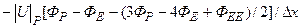 ;
;
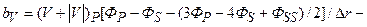
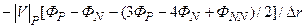
на этапе установления итераций мы повышаем порядок аппроксимации конвективных членов и схемы в целом до второго (относительно шагов по пространственным координатам) и тем самым минимизируем схемную вязкость. Фигурные скобки в (5.5.32) означают, что значения искомой функции берутся с предыдущей итерации. Интегрируя систему уравнений Навье-Стокса мы проходим все этапы присущие схеме решения задач приближения “узкого канала”, а именно получаем уравнения (5.5.12), (5.5.13), расщепляем продольную компоненту скорости по (5.5.15) и т.д. Однако в форме (5.5.16) вместо q( t, x, r) используем q1(t,x,r):
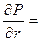 q1(t, x, r). (5.5.33)
q1(t, x, r). (5.5.33)
Здесь уже q1(t,x,r): содержит все члены, дополняющие (5.5.16) до полноценного уравнения импульсов в проекции на радиальную координату. Последовательность проведения расчетов состоит в следующем. Сначала находятся распределения (в выделенном сечении) окружной компоненты скорости { 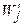 }, поскольку соответствующее ей уравнение не содержит градиента давления. Потом находятся [с использованием (5.5.16)] распределения {Zj}, далее по (20) {
}, поскольку соответствующее ей уравнение не содержит градиента давления. Потом находятся [с использованием (5.5.16)] распределения {Zj}, далее по (20) { 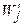 }, после чего по (5.5.15) {Uj}, затем по (5.5.23) П0 и {Пj} по (5.5.22) и, наконец, {Vj} из разностного аналога уравнения неразрывности. Далее переходим к другому сечению реализуя по существу маршевую процедуру вычислений (первый этап расчетов). В довершении всего с использованием (5.5.13) и прогонок в аксиальном направлении уточняем полученные распределения (второй этап). В качестве граничных условий в выходном сечении канала, необходимых для реализации второго этапа (продольных прогонок), берутся данные вычислений, полученных в конце первого этапа. Таким образом, по нашему алгоритму, как и в схеме расчетов, рекомендованной Патанкаром [2], физических граничных условий на выходе не требуется (требуется лишь, чтобы движение в выходном сечении было однонаправленным). Как видим в этом случае критерий Скарбороу (5.5.25) безусловно выполняется, что обеспечивает сходимость итерационных циклов. Получающаяся в результате расчетов схемная вязкость может быть минимизирована с использованием способа Рейсби [3].
}, после чего по (5.5.15) {Uj}, затем по (5.5.23) П0 и {Пj} по (5.5.22) и, наконец, {Vj} из разностного аналога уравнения неразрывности. Далее переходим к другому сечению реализуя по существу маршевую процедуру вычислений (первый этап расчетов). В довершении всего с использованием (5.5.13) и прогонок в аксиальном направлении уточняем полученные распределения (второй этап). В качестве граничных условий в выходном сечении канала, необходимых для реализации второго этапа (продольных прогонок), берутся данные вычислений, полученных в конце первого этапа. Таким образом, по нашему алгоритму, как и в схеме расчетов, рекомендованной Патанкаром [2], физических граничных условий на выходе не требуется (требуется лишь, чтобы движение в выходном сечении было однонаправленным). Как видим в этом случае критерий Скарбороу (5.5.25) безусловно выполняется, что обеспечивает сходимость итерационных циклов. Получающаяся в результате расчетов схемная вязкость может быть минимизирована с использованием способа Рейсби [3].
Заметим, что описанная численная процедура имеет преимущество в быстродействии в сравнении с алгоритмом, предложенным для решения аналогичных задач С. Патанкаром. Это обусловлено тем, что в нашем случае нет необходимости в использовании итерационного процесса по согласованию полей скорости и давления. Последнее стало возможным благодаря отказу от требования консервативности на уровне элементарной расчетной ячейки. Однако на участке стабилизированного течения схема становится консервативной. Кроме этого, всегда имеется баланс массы по сечению канала или камеры ибо это условие существенным образом используется при определении градиента давления. Во многих случаях этого оказывается более чем достаточно и решение получается близким к аналитическим распределениям локальных гидродинамических величин либо к экспериментальным данным.
Дата добавления: 2020-07-18; просмотров: 715;











