Дискретной случайной величины, закон Пуассона.

<1 2 345 6 7 >

Определение: Биномиальным называется закон распределения дискретной случайной величины Х- числа появлений события А в n независимых повторных испытаниях, в каждом из которых события А может наступить с вероятностью p или не наступить с вероятностью q=1-p. Тогда Р(Х=m)-вероятность появления события А ровно m раз в n испытаниях вычисляется по формуле Бернулли:

Р(Х=m)=С^m_np^mqⁿ^-^m

Математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной по бинарному закону, находят, соответственно, по формулам:

M(X)=np,

D(X)=npq,

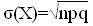
Если число испытаний n очень велико, а вероятность появления события А в каждом испытании очень мала (р≤0,1), то для вычисления Р(Х=m) используют формулу Пуассона:

Р(Х=m)=Р_n(m)= e^-^λ•λ^m , где λ=np

^m^!

Тогда говорят, что случайная величина Х - распределена по закону Пуассона.

Так как вероятность р события А в каждом испытании мала, то закон распределения Пуассона называется законом средних явлений.

Задача№3.Составить закон распределения случайной величины Х-числа выпадений пятерки при трех бросаниях игральной кости. Вычислить M(X),D(X), σ(Х) этой величины.

Решение: Испытание состоит в одном бросании игральной кости. Так как кость бросается 3 раза, то число испытаний n=3.

Вероятность события А - «выпадение пятерки» в каждом испытании одна и та же и равна 1/6, т.е. Р(А)=р=1/6, тогда Р(А)=1-p=q=5/6, где

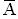- «выпадения не пятерки».

Случайная величина Х может принимать значения: 0;1;2;3.

Вероятность каждого из возможных значений Х найдем по формуле Бернулли:

Р(Х=0)=Р₃(0)=С⁰₃р⁰q³=1•(1/6)⁰•(5/6)³=125/216;

Р(Х=1)=Р₃(1)=С¹₃р¹q²=3•(1/6)¹•(5/6)²=75/216;

Р(Х=2)=Р₃(2)=С²₃р²q =3•(1/6)²•(5/6)¹=15/216;

Р(Х=3)=Р₃(3)=С³₃р³q⁰=1•(1/6)³•(5/6)⁰=1/216.

Т.о. закон распределения случайной величины Х имеет вид:

х

р 125/216 75/216 15/216 1/216

Контроль: 125/216+75/216+15/216+1/216=1.

Найдем числовые характеристики случайной величины Х:

M(X)=np=3•(1/6)=1/2,

D(X)=npq=3•(1/6) •(5/6)=5/12,

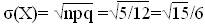
Задача№4.Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется:

а) 5 бракованных;

б) хотя бы одна бракованная.

Решение: Число n=1000 велико, вероятность изготовления бракованной детали р=0,002 мала, и рассматриваемые события (деталь окажется бракованной) независимы, поэтому имеет место формула Пуассона:

Р_n(m)= e^-^λ•λ^m

^m^!

Найдем λ=np=1000•0,002=2.

а)Найдем вероятность того, что будет 5 бракованных деталей (m=5):

Р₁₀₀₀(5)₌ e^-2•2⁵ ₌ 32•0,13534 ₌_0,0361

^{5 ! 120}

б)Найдем вероятность того, что будет хотя бы одна бракованная деталь.

Событие А -«хотя бы одна из отобранных деталей бракованная» является противоположным событию 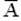-«все отобранные детали не бракованные».Следовательно, Р(А)=1-Р(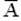). Отсюда искомая вероятность равна: Р(А)=1-Р₁₀₀₀(0)=1- e^-2•2⁰ ₌_1-_e^-2_{=1-0,13534≈0,865.}