Функция распределения

Полное описание случайной величины дает также функция распределения.

Определение: Функцией распределения дискретной случайной величины Хназывается функция F(x), определяющая для каждого значения х вероятность того, что случайная величина Х примет значение, меньше х:

F(x)=Р(Х<х)

Геометрически функция распределения интерпретируется как вероятность того, что случайная величина Х примет значение, которое изображается на числовой прямой точкой, лежащей левее точки х.

Свойства функции распределения:

1)0≤ F(x) ≤1;

2) F(x)- неубывающая функция на (-∞;+∞);

3) F(x)- непрерывна слева в точках х= x_i (i=1,2,…n) и непрерывна во всех остальных точках;

4) F(-∞)=Р (Х<-∞)=0 как вероятность невозможного события Х<-∞,

F(+∞)=Р(Х<+∞)=1 как вероятность достоверного события Х<-∞.

Если закон распределения дискретной случайной величины Х задан в виде таблицы:

то функция распределения F(x) определяется формулой:

0 при х≤ x_1,

р₁ при x₁< х≤ x_2,

F(x)= р₁ + р₂ при x₂< х≤ х₃

… … …

1 при х> х_n.

Её график изображен на рис.2:

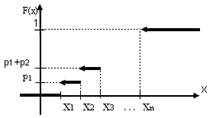
рис.2