Уравнение Пуассона и Лапласа. Теорема единственности решения

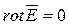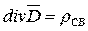Расчет электростатических полей с использованием уравнений и возможен только в простейших случаях. Наиболее общим методом является расчет электро­статических полей на основе решения уравнений Пуас­сона и Лапласа. Выве­дем эти уравне­ния.

Ранее было получено 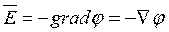. Подставим это выражение в уравнение ди­вергенции:

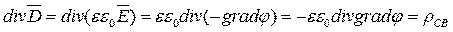, откуда следует:

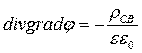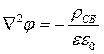или ― уравнение Пуассона.

Уравнение Пуассона справедливо для тех точек среды, где существуют объемные за­ряды .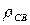

В реальных условиях свободные заряды располагаются на поверхности проводников бесконечно тонким слоем. Объемная плотность таких зарядов равна бесконечности и уравне­ние Пуассона применительно к ним теряет свой смысл.

В диэлектриках, которыми разделены заряженные проводники, объемные заряды от­сутствуют ( 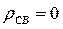), уравнение Пуассона превращается в уравнение Лапласа:

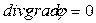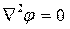или ― уравнение Лапласа.

Таким образом, электростатическое поле в диэлектрике описывается уравнением Лап­ласа, внутри проводников поле отсутствует вообще, а на гра­нице раздела диэлектрика с про­водником вступают в силу граничные усло­вия , .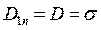

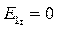В декартовой системе координат операцию двойного дифференцирова­ния 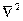записы­вают так:

.

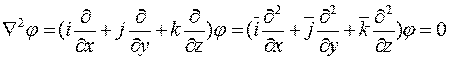Уравнение Лапласа в электростатике имеет исключительно важное значе­ние.

Уравнения Пуассона и Лапласа, как уравнения в частных производных, допускают множество линейно независимых частных решений. Однако в реаль­ных условиях каждой конкретной задаче соответствует только одно определен­ное решение.

Теорема единственности решения гласит, что найденное любым способом решение уравнений Пуассона или Лапласа, является единственно верным реше­нием, если оно удовле­творяет граничным условиям данной задачи.

Предположим, что существует два решения для вектора напряженности поля 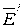и 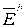, оба удовлетворяющие граничным условиям задачи. Тогда полу­чим:

.

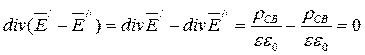
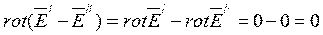Если rot и div от вектора равны нулю, то сам вектор тождественно равен нулю, следо­вательно 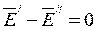, или 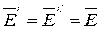, что требовалось доказать.

Из теоремы единственности решения вытекают два следствия, имеющее важное прак­тическое значение:

1) электростатическое поле в некотором объеме, ограниченном экви­потенциаль­ной поверхностью, не изменится, если эту поверхность заменить бесконечно тонким прово­дящим слоем;

2) электростатическое поле по одну сторону некоторой поверхности S не изме­нится, если по другую сторону поверхности изменить параметры среды (например, заменить поводящую среду диэлектриком) и изменить расположе­ние свободных зарядов так, чтобы на этой поверхности сохранились прежние граничные условия.

Второе следствие лежит в основе так называемого метода зеркальных отображений, применяемого на практике для расчета электростатических полей.