Уравнения электростатического поля в интегральной и дифференциальной форме
Интегральная форма уравнений описывает поле в конечных размерах объема, поверхности, линии, расположенных в пространстве. Дифференциальная форма тех же уравнений описывает поле в произвольных точках пространства.
1.Закон Кулона определяет силу взаимодействия между двумя точечными зарядами:
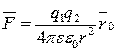 .
.
Сила взаимодействия двух точечных зарядов направлена по прямой, соединяющих эти заряды, при этом одноименные заряды отталкиваются, а разноименные - притягиваются.
2.Ранее была получена интегральная форма уравнения циркуляции вектора напряженности поля 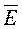 по замкнутому контуру:
по замкнутому контуру:
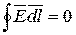 - интегральная форма.
- интегральная форма.
По теореме Стокса перейдем к дифференциальной форме этого уравнения:
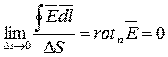 .
.
Так как площадка 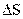 выбиралась произвольно, то очевидно проекция вектора
выбиралась произвольно, то очевидно проекция вектора 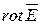 на любое направление равна нулю, следовательно и сам вектор равен нулю:
на любое направление равна нулю, следовательно и сам вектор равен нулю:
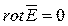 - дифференциальная форма.
- дифференциальная форма.
Ротор вектора 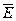 характеризует его вихри в пространстве. Равенство
характеризует его вихри в пространстве. Равенство 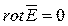 означает, что электростатическое поле является безвихревым, т.е. потенциальным.
означает, что электростатическое поле является безвихревым, т.е. потенциальным.
В декартовой системе координат операция rot запишется так:
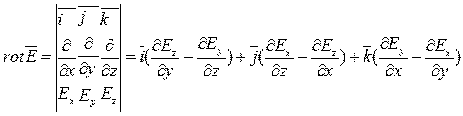 .
.
3. Теорема Гаусса является одной из фундаментальных теорем в теории поля:
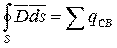 - интегральная форма записи теоремы гласит, что поток вектора электрического смещения
- интегральная форма записи теоремы гласит, что поток вектора электрического смещения 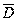 сквозь замкнутую поверхность S равен алгебраической сумме свободных зарядов, расположенные внутри поверхности S.
сквозь замкнутую поверхность S равен алгебраической сумме свободных зарядов, расположенные внутри поверхности S.
Для однородной среды 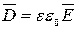 , тогда
, тогда 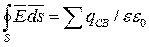 .
.
По теореме Остроградского перейдем к дифференциальной форме уравнения теоремы Гаусса:
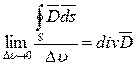 ,
, 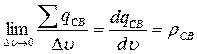 , следовательно:
, следовательно:
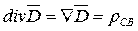 ― дифференциальная форма.
― дифференциальная форма.
Дивергенция вектора 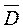 характеризует его истоки в пространстве, следовательно, линии вектора
характеризует его истоки в пространстве, следовательно, линии вектора 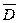 начинаются на положительных зарядах и заканчи- ваются на отрицательных.
начинаются на положительных зарядах и заканчи- ваются на отрицательных.
В декартовой системе координат операция div запишется так:
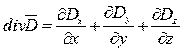 .
.
Для однородной среды 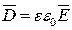 , тогда
, тогда 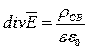 .
.
4. Электростатическое поле обладает способностью запасать энергию. Объемная плотность этой энергии выражается уравнением:
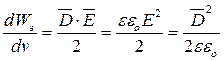 [Дж/м3].
[Дж/м3].
Для определения запаса энергии в заданном обьеме v необходимо выполнить интегрирование плотности энергии по заданному обьему:
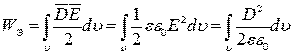 .
.
Дата добавления: 2020-07-18; просмотров: 534;











