Электростатическое поле осевых зарядов

Ниже будет рассмотрено несколько примеров электростатических полей, создаваемых осевыми зарядами.

1) Поле уединенной равномерно заряженной оси (рис. 257а).

Pасчет параметров поля в произвольной точке n выполним с помощью теоремы Гаусса в интегральной форме. Окружим ось цилиндром с произволь­ным радиусом r и длиной обра­зующей l =1. Вектор электрического смещения 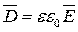в силу симметрии во всех точках на боковой поверхности цилиндра (r=const) имеет одно и то же значение и направление по ра­диусу, т.е. нормально к этой поверхности.

По теореме Гаусса получим:

.

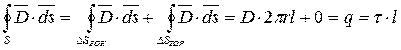Откуда следует, что .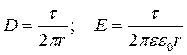

Поток вектора 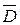через торцевые поверхности цилиндра равен нулю, так как линии вектора здесь направлены по касательной к поверхности.

В цилиндрической системе координат потенциал поля 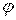будет зависеть только от ра­диуса r: 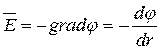, откуда

.

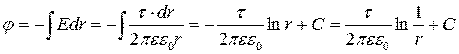Если принять на некоторой поверхности радиуса 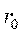значение потенциала равным нулю, то 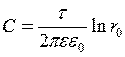и значение потенциала на поверхности произ­вольного радиуса бу­дет равна:

.

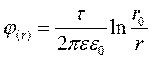2). Поле коаксиального кабеля (рис. 257б).

Конструктивно коаксиальный кабель состоит из внутреннего провода ра­диуса r₁ (прямой провод) и наружного провода в виде трубы или металличе­ского чехла радиуса r₂ (обратный провод), разделенных между собой диэлек­триком с относительной проницаемо­стью e.

Реальные заряды в коаксиальном кабеле расположены равномерно по по­верхности внутреннего провода (жиле) и на внутренней поверхности внешней оболочки. В соответствии со вторым следствием из теоремы единственности заменим поверхностные заряды внутрен­него провода осевым зарядом с линей­ной плотностью t, после чего к расчету параметров поля можно применить по­ложения и выводы, полученные ранее для заряженной оси:

.

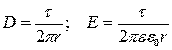Напряжение между внутренней жилой и оболочкой:

.

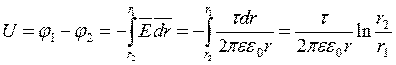Емкость кабеля на единицу длины:

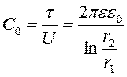, откуда следует, что .

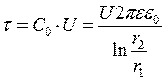Наибольшее значение напряженности поля имеет место на поверхности внутреннего провода при :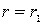

.

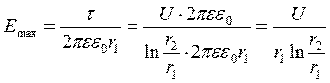3). Поле двух разноименно заряженных параллельных осей (рис. 258). Две двух разно­именно заряженные оси 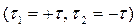расположены параллельно на расстоянии 2а в ди­электрическом пространстве.

Параметры поля в произвольной точке пространства n могут быть опреде­лены по ме­тоду наложения. Результирующий вектор напряженности поля ра­вен геометрической сумме составляющих, а результирующий потенциал – ал­гебраической сумме составляющих от каж­дого провода:

.

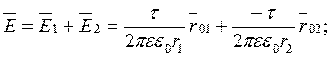
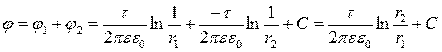Если принять 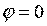в точках равноудалённых от обеих осей ( 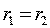), то постоянная интегрирования будет равна нулю (С=0), тогда получим:

.

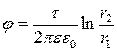Эквипотенциальные поверхности 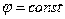должны удовлетворять усло­вию 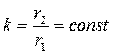. В геометрии есть малоизвестная теорема Аполония, которая гласит, что гео­метрическим местом точек, отношение расстояний от которых до заданной пары точек по­стоянно, является окружность, центр которой лежит на линии, соединяющей заданную пару точек. Эта окружность должна удовлетво­рять следующему условию:

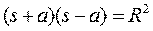или .

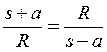Анализ геометрии рис. 2 показывает, что треугольник 20n подобен тре­угольнику n01 (общий угол с вершиной 0 и прилежащие к углу стороны про­порциональны). Из подобия треугольников следует:

.

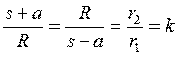При перемещении точки n вдоль окружности изменяются расстояния 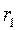и 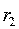так, что их отношение остается постоянным 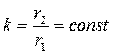. При изменении отношения 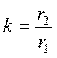центр окружности перемещается вдоль линии, соединяю­щую заданную пару точек 1 и 2. При k>1, 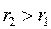и центр окружности нахо­диться в левой полуобласти, при k<1, 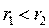и центр ок­ружно­сти находится в правой полуобласти, a при k=1, 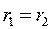, центр окружности смещается в беско­нечность, а сама окружность превращается в прямую линию, совпадающую с верти­кальной осью симметрии.

Линии вектора напряженности поля 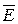также является дугами окружно­сти, но с цен­трами, расположенными на вертикальной оси симметрии.

Графической диаграммой или сеткой поля называется совокупность сле­дов эквипо­тенциальных поверхностей с заданными значениями потенциалов, построенная совместно с совокупностью следов линии вектора напряженности поля 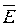. Графическая диаграмма поля двух разноименно заряженных осей имеет вид рис. 259.

По графической диаграмме поля можно определить его параметры ( 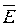, 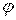) в любой точке.