Часть 3. Теория электромагнитного поля

Т1. Электростатическое поле

Основные понятия и определения

Электротехника ― это отрасль знаний об электромагнитных явлениях и их практиче­ском применении в технике. Физической основой всех электромаг­нитных явлений является электромагнитное поле.

Электромагнитное поле представляет собой вид материи, характеризую­щийся воздей­ствием на заряженные частицы. Как вид материи электромагнит­ное поле обладает массой, энергией, количеством движения, оно может пре­вращаться в вещество и наоборот.

Электромагнитное поле имеет две составляющие или две стороны - элек­трическую и магнитную. В каждой точке пространства оно определяется двумя векторными величинами: вектором напряженности электрического поля 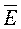[В/м] и вектором напряженности магнит­ного поля 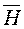[A/м].

Следует помнить, что в природе существует единое электромагнитное поле, а отдель­ные его стороны - электрическое или магнитное поле - могут проявляться независимо друг от друга только в частных случаях и при опреде­ленных условиях.

Электростатическое поле представляет собой частный случай электромаг­нитного поля. Оно создается системой неподвижных по отношению к наблюда­телю (в выбранной системе отсчета) зарядов.

Электрические заряды, создающие электростатическое поле, могут быть распределены в пространстве по тому или иному закону.

Если заряд q распределен в некотором объемеv, то он характеризуется объемной плотностью 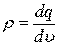[Кл/м³], откуда следует, что .

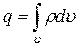Если заряд q распределен по некоторой поверхности s, то он характеризу­ется поверх­ностной плотностью 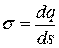[Кл/м²], откуда следует, что .

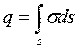Если заряд q распределен вдоль тонкого провода 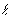или оси, то он харак­теризуется ли­нейной плотностью 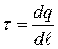[Кл/м], откуда следует, что .

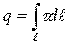И, наконец, если заряд q сосредоточен в точке, объем которой стремиться к нулю, то такой заряд называется точечным. Понятие точечного заряда явля­ется идеализированным, в природе точечных зарядов не существует, однако введение понятия точечного заряда имеет большое теоретическое значение.

Электростатическое поле в произвольной точке пространства характери­зуется векто­ром напряженности 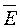[В/м]. Напряженность поля уединенного то­чечного заряда q определя­ется по формуле:

,

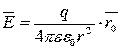где 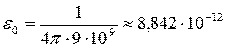[Ф/м] - диэлектрическая проницаемость пус­тоты; 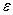- отно­сительная диэлектрическая проницаемость среды, показывающая во сколько раз проницае­мость данной среды больше проницаемости пус­тоты; 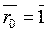- единичный радиус-вектор, на­правленный по радиусу от заряда, если q>0, и к заряду, если q<0 (рис. 254а).

Если электростатическое поле создается системой зарядов, то к расчету вектора на­пряженности 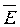применим принцип наложения, т.е. результирующее значение вектора на­пряженности поля 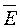в произвольной точке пространства будет равно геометрической сумме составляющих этого вектора от каждого то­чечного заряда в отдельности, т.е. 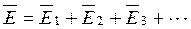. На рис.254б электро­статическое поле создается системой из двух точеч­ных зарядов ( 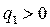и ). 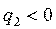Модуль результирующего вектора напряженности Е можно оп­ределить по формуле, вытекающей из теоремы косинусов:

.

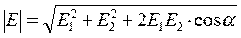Если электростатическое поле создается системой распределенных в про­странстве за­рядов, то эти заряды разбиваются на элементарные точечные за­ряды dq, а операция сложения заменяется интегрированием по объему, площади или длине, в зависимости от того, как рас­пределены заряды в пространстве.

Пусть точечный заряд q перемещается в электростатическом поле 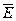из точки 1 в точку 2 по произвольной траектории 1а2 (рис. 255.)

При перемещении заряда будет совершаться некоторая работа:

.

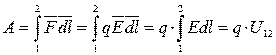Напряжением между точками 1 и 2 называется отношение работы по пе­ремещению заряда из точки 1 в точку 2 к величине заряда q:

.

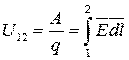Если переместить заряд обратно в точку 1 по некоторой новой траектории 2b1, то со­гласно закону сохранения энергии суммарная работа по перемеще­нию заряда будет равна нулю:

.

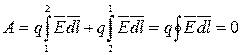Из полученного выражения следует два вывода:

1) 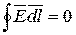- циркуляция вектора напряженности поля 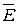по замкнутому контуру равна нулю;

2) 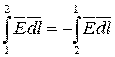или 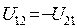- напряжение между двумя точками 1 и 2 не зави­сит от выбора пути интегрирования.

Второй вывод позволяет ввести в расчет некоторую функцию координат 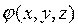под названием потенциала поля, разность значений которой в рас­сматриваемых точках 1 и 2 чис­ленно равна напряжению между этими точками:

.

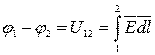Пусть потенциал точки 1 известен ( 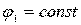), а точка 2 перемещается в простран­стве и ее потенциал будет функцией координат x, y, z:

.

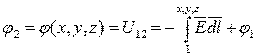В электротехнике за базовую точку с заданным нулевым потенциалом принимают “землю”, а при отсутствии заземления - любую точку цепи или схемы.

Принимая 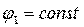за постоянную интегрирования, перейдем к неопре­деленному интегралу:

,

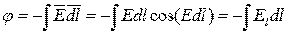откуда 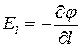, т.е. проекция вектора 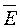на любое направление l показывает скорость убы­вания потенциала в этом направлении. Аналогично можно запи­сать составляющие век­тора 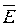по координатным осям x, y, z:

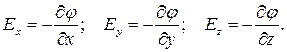
Просуммируем отдельные составляющие вектора:

,

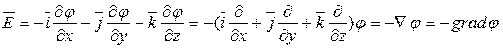где 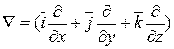- оператор пространственного дифференцирования (Гамиль­тона).

Поверхность, на которой потенциал 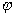имеет постоянное значение, назы­вается экви­потенциальной. Вектор напряженности поля 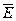направлен в сторону наибольшего убывания потенциала и, следовательно, перпендикулярно к экви­потенциальной поверхности.