Электростатическое поле и емкость двухпроводной линии
Пусть требуется рассчитать электростатическое поле и емкость двухпроводной линии с заданными геометрическими размерами (радиус проводов R, межосевое расстояние d, радиус R соизмерим с расстоянием d). Провода линии не заземлены, к линии приложено постоянное напряжение U (рис. 260).
Согласно второму следствию из теоремы единственности заменим поверхностные заряды проводов осевыми +t и -t, проводящую среду - диэлектриком так, чтобы на поверхности проводов сохранились прежние условия, а именно: эти поверхности должны остаться эквипотенциальными с теми же значениями потенциалов 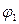 = +j и
= +j и 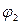 = -j. Чтобы выполнить эти условия, электрические оси проводов должны быть смещены относительно геометрических осей на некоторое расстояние s- a.
= -j. Чтобы выполнить эти условия, электрические оси проводов должны быть смещены относительно геометрических осей на некоторое расстояние s- a.

Согласно второму следствию из теоремы единственности заменим поверхностные заряды проводов осевыми +t и -t, проводящую среду - диэлектриком так, чтобы на поверхности проводов сохранились прежние условия, а именно: эти поверхности должны остаться эквипотенциальными с теми же значениями потенциалов 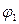 = +j и
= +j и 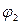 = -j. Чтобы выполнить эти условия, электрические оси проводов должны быть смещены относительно геометрических осей на некоторое расстояние s- a.
= -j. Чтобы выполнить эти условия, электрические оси проводов должны быть смещены относительно геометрических осей на некоторое расстояние s- a.
Положение электрических осей определяется из теоремы Аполония:
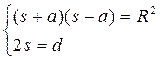
Таким образом, электростатическое поле, создаваемое двумя проводами с поверхностными зарядами σ, будет эквивалентным полю, которое создается двумя разноименно заряженными осями +t и -t, и для его расчета можно применить полученные ранее формулы:
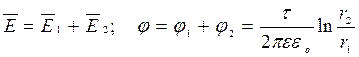
Потенциал положительного провода:
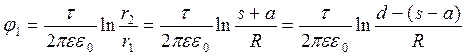 .
.
В силу симметрии 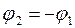 , тогда напряжение:
, тогда напряжение:
U = 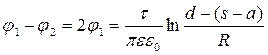 ,
,
где s-a – смещение электрической оси провода относительно геометрической.
Из полученного выражения вытекают расчетные формулы:
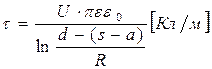 ;
; 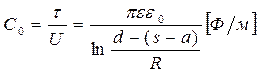 .
.
Для воздушных линий ( 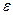 =1) межосевое расстояние d многократно больше радиуса проводов R. В этом случае смещением электрических осей можно пренебречь (s-a
=1) межосевое расстояние d многократно больше радиуса проводов R. В этом случае смещением электрических осей можно пренебречь (s-a 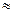 0) и считать, что электрические оси проводов совпадают с геометрическими. Для таких линий полученные выше расчетные формулы будут иметь вид:
0) и считать, что электрические оси проводов совпадают с геометрическими. Для таких линий полученные выше расчетные формулы будут иметь вид:
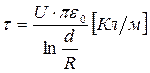 ,
, 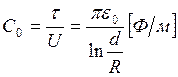 .
.
Дата добавления: 2020-07-18; просмотров: 575;











