Нелинейная катушка с сердечником на переменном токе

Рассмотрим физические процессы, протекающие в катушке с сердечни­ком на пере­менном токе (рис. 231а).

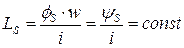Протекающий по обмотке w ток i создает магнитный поток ф, большая часть кото­рого (основной поток) ф_о замыкается по сердечнику, и незначитель­ная часть (поток рас­сеяния) ф_s – по воздуху. Основной поток ф_о нелинейно за­висит от тока i, а поток рассея­ния пропорционален току, следовательно: – индуктивность рас­сеяния.

Протекающий по обмотке w ток i создает магнитный поток ф, большая часть кото­рого (основной поток) ф_о замыкается по сердечнику, и незначитель­ная часть (поток рас­сеяния) ф_s – по воздуху. Основной поток ф_о нелинейно за­висит от тока i, а поток рассея­ния пропорционален току, следовательно: 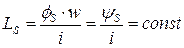– индуктивность рас­сеяния.

Электрическое состояние цепи можно описать нелинейным дифферен­циальным уравнением:

.

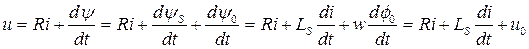При синусоидальном напряжении на зажимах искажения форм кривых других пе­ременных (i, ф 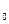) будут незначительны, поэтому для исследование ре­жима катушки можно применить метод эквивалентных синусоид.

Уравнение цепи в комплексной форме получит вид:

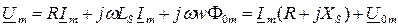- для комплексных амплитуд;

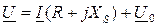- для комплексных действующих значений.

Данному уравнению соответствует эквивалентная схема замещения ка­тушки с сер­дечником (рис. 231б), в которой приняты следующие обозначения: R, X_S - активное и реактив­ное (рассеяния) сопротивления обмотки катушки; G 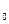, B 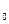- актив­ная и реактивная проводи­мости, вносимые сердечником, значения ко­торых для конкретной катушки определяются через мощность потерь в сердеч­нике ( 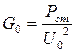) и намагничиваю­щуюся мощность ( ).

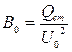Векторная диаграмма для схемы замещения показана на рис. 232:

Вследствие наличия потерь в сердечнике, магнитный поток Ф 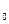будет от­ставать от тока I на угол a, который принято называть углом потерь.