Трансформатор с сердечником и его схема замещения

Картина распределения магнитных потоков в трансформаторе с сердеч­ником пока­зана на рис. 233:

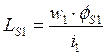- индуктивность рассеяния первичной обмотки,

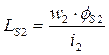- индуктивность рассеяния вторичной обмотки.

Основной поток ф 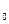, замыкающийся по сердечнику, создается с суммар­ной МДС, с которой он связан нелинейно: .

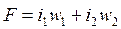Дифференциальные уравнения для первичной и вторичной цепей:

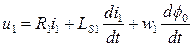
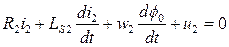
Введем обозначения: 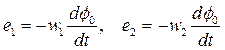, тогда уравнения при­мут вид:

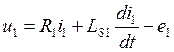
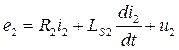
Анализ полученных уравнений показывает, что ЭДС в первичной цепи e 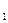направ­лена навстречу приложенному уравнению u 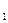и уравновешивает боль­шую его часть, т.е. иг­рает роль противодействующей ЭДС, а ЭДС во вторичной цепи 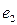создает ток 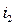, т.е. играет роль генераторной ЭДС.

Применим к уравнениям трансформатора методом эквивалентных сину­соид и за­пишем их в комплексной форме:

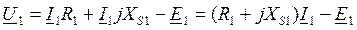
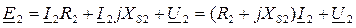
Если числа витков обмоток существенно отличаются, т.е. коэффициент трансфор­мации 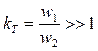, то все переменные величины вторичной цепи «приводят» к первичной цепи. Приведение заключается в замене реального трансформатора с 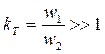эквива­лентным расчетным трансформатором с коэффициентом трансформации 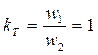. Все приведенные величины обо­значаются штрихом сверху. Условием эквивалентности приве­денной схемы яв­ляются:

1) сохранение без изменения намагничивающей силы ;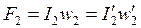

2) сохранение без изменения мощности .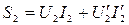

Формулы приведения:

1) 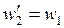- согласно условию;

2) ;

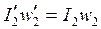
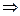
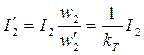3) ;

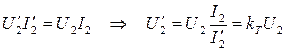4) ;

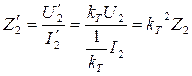5) .

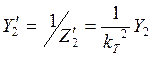Уравнения приведенного трансформатора получат вид:

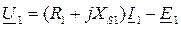
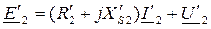
Этим уравнениям соответствует схема замещения (рис. 234):

Основной магнитный поток Ф 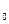создается суммой МДС обеих обмоток. По закону Ома для магнитной цепи:

= ,

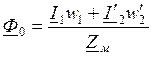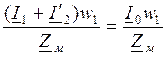где Z_м - комплексное магнитное сопротивление сердечника, 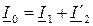- суммарный намагничивающий ток, равный току холостого хода. Из получен­ного уравнения следует:

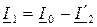, т.е. ток первичной цепи трансформатора равен сумме тока холо­стого хода I 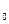и приведенного вторичного тока с обратным знаком (- ).

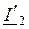Векторная диаграмма токов и напряжений для приведенного трансфор­матора пока­зана на рис. 235.